
Quantum wires in one dimension: disorder,electronic transportand
... to classical analogues [183, 114], in particular to chaotic systems of oscillators where quantum localization can be understood in terms of energetic stability of phase-space orbits of the classical system [177]. Anderson proved for his model (the Anderson model) that the system in 3-D registers a M ...
... to classical analogues [183, 114], in particular to chaotic systems of oscillators where quantum localization can be understood in terms of energetic stability of phase-space orbits of the classical system [177]. Anderson proved for his model (the Anderson model) that the system in 3-D registers a M ...
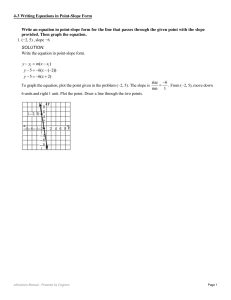
Write an equation in point-slope form for the line that passes through
... Sample answer: Depending on what information is given and what the problem is, it might be easier to represent a linear equation in one form over another. For example, if you are given the slope and the y-intercept, you could represent the equation in slope-intercept form. A line that has a slope of ...
... Sample answer: Depending on what information is given and what the problem is, it might be easier to represent a linear equation in one form over another. For example, if you are given the slope and the y-intercept, you could represent the equation in slope-intercept form. A line that has a slope of ...
Quantum Physics of Nature QuPoN 2015 Book of Abstracts
... with high spatial resolution, which, e.g., can be used to project complex holograms. Modern LC-SLMs additionally allow to modulate the reflected phase front by several multiples of a wavelength. These "thick" phase patterns have similar properties as volume holograms, showing wavelength and angular ...
... with high spatial resolution, which, e.g., can be used to project complex holograms. Modern LC-SLMs additionally allow to modulate the reflected phase front by several multiples of a wavelength. These "thick" phase patterns have similar properties as volume holograms, showing wavelength and angular ...
BASIS SET SUPERPOSITION ERROR EFFECTS, EXCITED-STATE POTENTIAL ENERGY SURFACE AND
... The study of the photophysics of thymine is the main objective of this thesis. This work has been divided in 4 parts; the first two parts are devoted to find a proper level of theory for the study of thymine, whereas in the third and fourth parts the photohpysics of thymine are studied. Moran et al. ...
... The study of the photophysics of thymine is the main objective of this thesis. This work has been divided in 4 parts; the first two parts are devoted to find a proper level of theory for the study of thymine, whereas in the third and fourth parts the photohpysics of thymine are studied. Moran et al. ...
Studies of Infinite Two-Dimensional Quantum Lattice
... Determining the properties of quantum many-body systems is a central challenge in modern physics. Being able to determine the macroscopic properties of a system from its microscopic description would hasten progress in many fields of science and technology. However, we currently lack the tools to so ...
... Determining the properties of quantum many-body systems is a central challenge in modern physics. Being able to determine the macroscopic properties of a system from its microscopic description would hasten progress in many fields of science and technology. However, we currently lack the tools to so ...
Quantum Computing - Department of Computing
... of nature as it predicts quantum effects up to an astonishing precision of 14 decimal places. But we do not know why nature works like that and why quantum mechanics gives such a good description of nature. In other words, quantum mechanics tells us how things work but cannot tell us why they work t ...
... of nature as it predicts quantum effects up to an astonishing precision of 14 decimal places. But we do not know why nature works like that and why quantum mechanics gives such a good description of nature. In other words, quantum mechanics tells us how things work but cannot tell us why they work t ...
Quantum Nonlinear Optics in Lossy Coupled-Cavities in Photonic Crystal Slabs
... of the high Q and the small V is of great importance in many applications in integrated photonics. There are other optical microcavities that can perform better than PCS microcavities, but only in certain aspects. For example, whispering gallery microtoroids and microspheres can support modes with v ...
... of the high Q and the small V is of great importance in many applications in integrated photonics. There are other optical microcavities that can perform better than PCS microcavities, but only in certain aspects. For example, whispering gallery microtoroids and microspheres can support modes with v ...
Boundary conditions for integrable quantum systems
... At present, a number of one-dimensional quantum integrable models are known which are soluble by means of the Bethe ansatz (Gaudin 1983) or the quantum inverse scattering method (QISM) (see Faddeev 1984, Kulish and Sklyanin 1982). The best studied cases are those of the infinite interval and of the ...
... At present, a number of one-dimensional quantum integrable models are known which are soluble by means of the Bethe ansatz (Gaudin 1983) or the quantum inverse scattering method (QISM) (see Faddeev 1984, Kulish and Sklyanin 1982). The best studied cases are those of the infinite interval and of the ...
Theoretical and experimental status of magnetic monopoles
... electric fields. This was only possible if the product of electric and magnetic charges was quantized. This prediction was an example of what Gell-Mann would later call the “totalitarian principle” – that anything which is not forbidden is compulsory [10]. Dirac eventually became disillusioned with t ...
... electric fields. This was only possible if the product of electric and magnetic charges was quantized. This prediction was an example of what Gell-Mann would later call the “totalitarian principle” – that anything which is not forbidden is compulsory [10]. Dirac eventually became disillusioned with t ...
Adiabatic Circuits and Reversible Computing - UF CISE
... little entropy need be produced, and arbitrarily little free energy need be used up. Of course, in practice, there are other sources of entropy generation such as leakage, frictional effects, and the finite quality factor Q of all real-world processes. But, we know of no fundamental lower bounds tha ...
... little entropy need be produced, and arbitrarily little free energy need be used up. Of course, in practice, there are other sources of entropy generation such as leakage, frictional effects, and the finite quality factor Q of all real-world processes. But, we know of no fundamental lower bounds tha ...
Lectures in Theoretical Biophysics - Theoretical and Computational
... course, so large that solutions of Eq. (2.1) for macroscopic systems are impossible. In microscopic systems like proteins the number of atoms ranges between 103 to 105 , i.e., even in this case the solution is extremely time consuming. However, most often only a few of the degrees of freedom are inv ...
... course, so large that solutions of Eq. (2.1) for macroscopic systems are impossible. In microscopic systems like proteins the number of atoms ranges between 103 to 105 , i.e., even in this case the solution is extremely time consuming. However, most often only a few of the degrees of freedom are inv ...
Polynomial Heisenberg algebras and Painleve
... potencial del oscilador invertido [Bermudez and Fernández, 2013b]. Posteriormente, presentaremos las definiciones del álgebra de Heisenberg-Weyl y de las álgebras de Heisenberg polinomiales (PHA). Estudiaremos los sistemas generales descritos por PHA: para órdenes cero y uno obtenemos a los osci ...
... potencial del oscilador invertido [Bermudez and Fernández, 2013b]. Posteriormente, presentaremos las definiciones del álgebra de Heisenberg-Weyl y de las álgebras de Heisenberg polinomiales (PHA). Estudiaremos los sistemas generales descritos por PHA: para órdenes cero y uno obtenemos a los osci ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.














![Edward Wilson-Ewing, 23rd February 2015 [PDF 1.69MB]](http://s1.studyres.com/store/data/018149793_1-f86d120fe9b970cd94dca9a182a1667d-300x300.png)







