Lesson 16-1
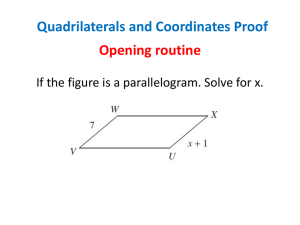
... Quadrilaterals and Coordinates Proof Re-teach MAFS.912.G-CO.3.10: Prove theorems about triangles; use theorems about triangles to solve problems. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints ...
... Quadrilaterals and Coordinates Proof Re-teach MAFS.912.G-CO.3.10: Prove theorems about triangles; use theorems about triangles to solve problems. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints ...
A Formula for the Intersection Angle of Backbone Arcs with the
... The central angle, α, made by the radius OB with the xaxis is the complement of ω (which can be seen since the equidistant circle is symmetric across the perpendicular bisector of OB). Thus yint = sin α = cos ω, so that ...
... The central angle, α, made by the radius OB with the xaxis is the complement of ω (which can be seen since the equidistant circle is symmetric across the perpendicular bisector of OB). Thus yint = sin α = cos ω, so that ...
Use the Geometry Calculator
... a point. The vector defines the direction of the normal, not a location in space. You can add this normal vector to a point to obtain another point. nor Determines the three-dimensional unit normal vector of a selected circle, arc, or polyline arc segment. This normal vector is the Z coordinate of t ...
... a point. The vector defines the direction of the normal, not a location in space. You can add this normal vector to a point to obtain another point. nor Determines the three-dimensional unit normal vector of a selected circle, arc, or polyline arc segment. This normal vector is the Z coordinate of t ...
Coordinate Geometry
... line intersects the x axis. In order to find the y intercept, simply set x = 0 and solve for the value of y . To find the x intercept, set y = 0 and solve for x . To sketch a line given in slopeintercept form, first plot the y intercept, and then use the slope of the line to plot another poin ...
... line intersects the x axis. In order to find the y intercept, simply set x = 0 and solve for the value of y . To find the x intercept, set y = 0 and solve for x . To sketch a line given in slopeintercept form, first plot the y intercept, and then use the slope of the line to plot another poin ...
Slide 1
... You can find the horizontal distance subtracting the xcoordinates of points A and B: AC = |7 – 2| = 5. Similarly, to find the vertical distance BC, subtract the ycoordinates of points A and B: BC = |8 – 1| = 7. Now you can use the Pythagorean Theorem to find AB. ...
... You can find the horizontal distance subtracting the xcoordinates of points A and B: AC = |7 – 2| = 5. Similarly, to find the vertical distance BC, subtract the ycoordinates of points A and B: BC = |8 – 1| = 7. Now you can use the Pythagorean Theorem to find AB. ...
A rigorous deductive approach to elementary Euclidean geometry
... given physical quantity with greater and greater accuracy. Square roots are forced upon us by Pythagoras’ theorem, and computing their numerical values is also a very good introduction to the concept of real number. I would certainly recommend to (re)introduce from the very start of junior high scho ...
... given physical quantity with greater and greater accuracy. Square roots are forced upon us by Pythagoras’ theorem, and computing their numerical values is also a very good introduction to the concept of real number. I would certainly recommend to (re)introduce from the very start of junior high scho ...
lecture 2
... Curves arise in many applications such as art, industrial design, mathematics, architecture, and engineering, and numerous computer drawing packages and computeraided design packages have been developed to facilitate the creation of curves. A particularly illustrative application is that of computer ...
... Curves arise in many applications such as art, industrial design, mathematics, architecture, and engineering, and numerous computer drawing packages and computeraided design packages have been developed to facilitate the creation of curves. A particularly illustrative application is that of computer ...
Perspective Projection
... OpenGL with a call to glVertex*() or glVertexPointer(). They represent the coordinates of your object or other geometry you want to render. • Many programmers use a World Coordinate system. – Objects are often modeled in one coordinate system, then scaled, translated, and rotated into the world you' ...
... OpenGL with a call to glVertex*() or glVertexPointer(). They represent the coordinates of your object or other geometry you want to render. • Many programmers use a World Coordinate system. – Objects are often modeled in one coordinate system, then scaled, translated, and rotated into the world you' ...
Vector Geometry for Computer Graphics
... Given a polygon (which by definition lies in a plane) and a single point in the same plane, we would like an algorithm for determining whether the point lies inside the polygon. The following algorithm only applies to convex polygons – those with the property that given any two points inside the pol ...
... Given a polygon (which by definition lies in a plane) and a single point in the same plane, we would like an algorithm for determining whether the point lies inside the polygon. The following algorithm only applies to convex polygons – those with the property that given any two points inside the pol ...
Vector Geometry for Computer Graphics
... Given a polygon (which by definition lies in a plane) and a single point in the same plane, we would like an algorithm for determining whether the point lies inside the polygon. The following algorithm only applies to convex polygons – those with the property that given any two points inside the pol ...
... Given a polygon (which by definition lies in a plane) and a single point in the same plane, we would like an algorithm for determining whether the point lies inside the polygon. The following algorithm only applies to convex polygons – those with the property that given any two points inside the pol ...
vector - Games @ UCLAN
... Imagine that you want to move something by a given distance in a particular direction. We multiply the direction vector by the distance we want to move. For example, move the normalised vector ( 2, 4, 5 ) by 12 units results in ( 24, 48, 60 ) ...
... Imagine that you want to move something by a given distance in a particular direction. We multiply the direction vector by the distance we want to move. For example, move the normalised vector ( 2, 4, 5 ) by 12 units results in ( 24, 48, 60 ) ...
TWO CAMERAS 2009
... perspective are known for many years, the mathematicians investigate them now in the framework of the projective, affine and Euclidian geometry to obtain more efficient and elegant results. In this context we present here the main law for central projection in projective coordinate system and applic ...
... perspective are known for many years, the mathematicians investigate them now in the framework of the projective, affine and Euclidian geometry to obtain more efficient and elegant results. In this context we present here the main law for central projection in projective coordinate system and applic ...