Partial Metric Spaces
... Q1: if x = y then q(x, y) = 0 (equality implies indistancy), and Q4: q(x, z) ≤ q(x, y) + q(y, z) (triangularity). A quasimetric space is called t0 if it also satisfies: Q2: if q(x, y) = q(y, x) = 0 then x = y (indistancy implies equality). Unsurprisingly, for a quasimetric space (X, q), f : X → X is ...
... Q1: if x = y then q(x, y) = 0 (equality implies indistancy), and Q4: q(x, z) ≤ q(x, y) + q(y, z) (triangularity). A quasimetric space is called t0 if it also satisfies: Q2: if q(x, y) = q(y, x) = 0 then x = y (indistancy implies equality). Unsurprisingly, for a quasimetric space (X, q), f : X → X is ...
Holographic dual of a time machine
... considering “timelike” quasigeodesics. But due to the lensing timelike separated points can be also connected by continuous spacelike geodesics. The latter are directly related to the entanglement. So, do we have a state with a high rate of timelike entanglement on the boundary?.. (see also S. O ...
... considering “timelike” quasigeodesics. But due to the lensing timelike separated points can be also connected by continuous spacelike geodesics. The latter are directly related to the entanglement. So, do we have a state with a high rate of timelike entanglement on the boundary?.. (see also S. O ...
"Here`s to Looking at Euclid" A Snapshot of Hyperbolic Geometry
... having the segment as radius and one endpoint as center. 4. All right angles are congruent. 5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side ...
... having the segment as radius and one endpoint as center. 4. All right angles are congruent. 5. If two lines are drawn which intersect a third in such a way that the sum of the inner angles on one side is less than two right angles, then the two lines inevitably must intersect each other on that side ...
Strange Geometries
... familiar with: that the angles in a triangle add up to 180 degrees. However, this postulate did not seem as obvious as the other four on Euclid’s list, so mathematicians attempted to deduce it from them: to show that a geometry obeying the first four postulates would necessarily obey the fifth. Thei ...
... familiar with: that the angles in a triangle add up to 180 degrees. However, this postulate did not seem as obvious as the other four on Euclid’s list, so mathematicians attempted to deduce it from them: to show that a geometry obeying the first four postulates would necessarily obey the fifth. Thei ...
File
... so as to form equal alternate interior angles or corresponding angles, then the lines are parallel with a common perpendicular. Theorem 1-9: If two lines have a common perpendicular, there exists transversals, other than the perpendicular, which cut the lines so as to form equal alternate interior ...
... so as to form equal alternate interior angles or corresponding angles, then the lines are parallel with a common perpendicular. Theorem 1-9: If two lines have a common perpendicular, there exists transversals, other than the perpendicular, which cut the lines so as to form equal alternate interior ...
MA651 Topology. Lecture 11. Metric Spaces 2.
... Theorem 65.1. Let (E, d) be a metric space. Then a metric space (Ê, δ) can be constructed with the following properties: 1. There is a biuniform correspondence between E and a subset of Ê 2. If we identify E and this subset of Ê, the distance induced by δ on E in d, and E in dense in Ê. 3. (Ê, ...
... Theorem 65.1. Let (E, d) be a metric space. Then a metric space (Ê, δ) can be constructed with the following properties: 1. There is a biuniform correspondence between E and a subset of Ê 2. If we identify E and this subset of Ê, the distance induced by δ on E in d, and E in dense in Ê. 3. (Ê, ...
Lectures in Discrete Differential Geometry 3
... naturally suggests a definition of mean curvature defined on mesh edges instead of vertices: we could build up a notion of discrete functions on edges, together with an inner product, and formalize this idea. We won’t go into the details here, but this would lead to a hinge-based formula, linear in ...
... naturally suggests a definition of mean curvature defined on mesh edges instead of vertices: we could build up a notion of discrete functions on edges, together with an inner product, and formalize this idea. We won’t go into the details here, but this would lead to a hinge-based formula, linear in ...
Slides
... Let φ ≡ ∃x1 , . . . , xn . ∀ȳ /Qz̄. ψ. Thanks to previous theorem, φ is satisfiable iff exists an interpretation of x1 , . . . , xn in a metric space M with at most max(n, 1) points satisfying ∀ȳ /Qz̄. ψ. By replacing every subformula of φ of the form ∀y . ψ with the conjunction ψ[x1 /y ] ∧ · · · ...
... Let φ ≡ ∃x1 , . . . , xn . ∀ȳ /Qz̄. ψ. Thanks to previous theorem, φ is satisfiable iff exists an interpretation of x1 , . . . , xn in a metric space M with at most max(n, 1) points satisfying ∀ȳ /Qz̄. ψ. By replacing every subformula of φ of the form ∀y . ψ with the conjunction ψ[x1 /y ] ∧ · · · ...
histm008b
... for suitable integers a, b, c. Aristotle claimed that the only solid regular polyhedra which fill space in a regular manner are the cube and the regular tetrahedron, but he did not give reasons for his assertion. Between the time of Aristotle and the late 15th century, there were many attempts to un ...
... for suitable integers a, b, c. Aristotle claimed that the only solid regular polyhedra which fill space in a regular manner are the cube and the regular tetrahedron, but he did not give reasons for his assertion. Between the time of Aristotle and the late 15th century, there were many attempts to un ...
ANS - JMap
... The formulas that you may need to answer some questions in this examination are found at the end of the examination. This sheet is perforated so you may remove it from this booklet. Scrap paper is not permitted for any part of this examination, but you may use the blank spaces in this booklet as scr ...
... The formulas that you may need to answer some questions in this examination are found at the end of the examination. This sheet is perforated so you may remove it from this booklet. Scrap paper is not permitted for any part of this examination, but you may use the blank spaces in this booklet as scr ...
§1: FROM METRIC SPACES TO TOPOLOGICAL SPACES We
... This construction gives us a way of speaking about continuous functions and convergent sequences on the Cartesian product X. But it is certainly not a very natural construction. Fundamentally, the problem is that given a collection (Xα , dα )α∈I of metric spaces, no natural metric presents itself on ...
... This construction gives us a way of speaking about continuous functions and convergent sequences on the Cartesian product X. But it is certainly not a very natural construction. Fundamentally, the problem is that given a collection (Xα , dα )α∈I of metric spaces, no natural metric presents itself on ...
Metric properties versus topological ones
... that B(x, ǫ) ⊂ U . Since xn → x, we find nǫ such that d(xn , x) < ǫ/2 for all n > nǫ . Using the triangle inequality, we deduce that B(xn , ǫ/2) ⊂ U for all n ≥ nǫ . Choosing n so that also 1/2n < ǫ/2, we deduce that B(xn , 1/2n ) ⊂ U , which contradicts the fact that B(xn , 21n ) cannot be covered ...
... that B(x, ǫ) ⊂ U . Since xn → x, we find nǫ such that d(xn , x) < ǫ/2 for all n > nǫ . Using the triangle inequality, we deduce that B(xn , ǫ/2) ⊂ U for all n ≥ nǫ . Choosing n so that also 1/2n < ǫ/2, we deduce that B(xn , 1/2n ) ⊂ U , which contradicts the fact that B(xn , 21n ) cannot be covered ...
Symmetric Spaces
... First consider the Grassmannian of oriented k-planes in Rk+l , denoted by M = G̃k (Rk+l ). Thus, each element in M is a k-dimensional subspace of Rk+l together with an orientation. We shall assume that we have the orthogonal splitting Rk+l = Rk ⊕ Rl , where the distinguished element p = Rk takes up ...
... First consider the Grassmannian of oriented k-planes in Rk+l , denoted by M = G̃k (Rk+l ). Thus, each element in M is a k-dimensional subspace of Rk+l together with an orientation. We shall assume that we have the orthogonal splitting Rk+l = Rk ⊕ Rl , where the distinguished element p = Rk takes up ...
Document
... Gravity, Space, and a New Geometry • According to the principle of equivalence, the rotating disk is equivalent to a stationary disk with a strong gravitational field near its edge and a weaker gravitational field toward its center. • Measurements of distance, then, will depend on the strength of g ...
... Gravity, Space, and a New Geometry • According to the principle of equivalence, the rotating disk is equivalent to a stationary disk with a strong gravitational field near its edge and a weaker gravitational field toward its center. • Measurements of distance, then, will depend on the strength of g ...
Part I Linear Spaces
... 3. If there is some geometry (i.e. the topology is metrizable) then compactness is equivalent to sequential compactness, which states that for any sequence there is a subsequence that converges. 4. Net convergence: Without geometry, one needs to use more than sequences. A net (xα )α∈I is a collectio ...
... 3. If there is some geometry (i.e. the topology is metrizable) then compactness is equivalent to sequential compactness, which states that for any sequence there is a subsequence that converges. 4. Net convergence: Without geometry, one needs to use more than sequences. A net (xα )α∈I is a collectio ...
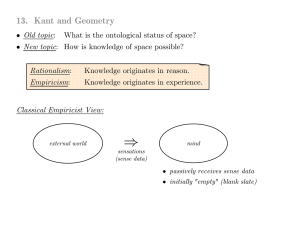
13.Kant and Geometry
... "The apodeictic certainty of all geometrical propositions, and the possibility of their a priori construction, is grounded in this a priori necessity of space. Were this representation of space a concept acquired a posteriori, and derived from outer experience in general, the first principles of mat ...
... "The apodeictic certainty of all geometrical propositions, and the possibility of their a priori construction, is grounded in this a priori necessity of space. Were this representation of space a concept acquired a posteriori, and derived from outer experience in general, the first principles of mat ...
On the density of the hyperspace of a metric space
... ℵ0 , and will prove to be extremely useful in the following. Theorem 7. A metrizable space X is GK if and only if it has no closed and discrete subset of cardinality equal to dX. Proof: First, suppose that there exists a closed and discrete subset D of X with |D| = dX = ν. By Hausdorff’s extension t ...
... ℵ0 , and will prove to be extremely useful in the following. Theorem 7. A metrizable space X is GK if and only if it has no closed and discrete subset of cardinality equal to dX. Proof: First, suppose that there exists a closed and discrete subset D of X with |D| = dX = ν. By Hausdorff’s extension t ...
Branches of differential geometry
... isometry. This notion can also be defined locally, i.e. for small neighborhoods of points. Any two regular curves are locally isometric. However, Theorema Egregium of Gauss showed that already for surfaces, the existence of a local isometry imposes strong compatibility conditions on their metrics: t ...
... isometry. This notion can also be defined locally, i.e. for small neighborhoods of points. Any two regular curves are locally isometric. However, Theorema Egregium of Gauss showed that already for surfaces, the existence of a local isometry imposes strong compatibility conditions on their metrics: t ...
ppt
... and a commutative associative operation m where the compositite of two letters is a set of letters. The identity is a subset e of the alphabet. ...
... and a commutative associative operation m where the compositite of two letters is a set of letters. The identity is a subset e of the alphabet. ...
Geometry H
... SA & V of Spheres Definition of a sphere: The distance from the center to the sphere is called the __________. A segment passing thru the center connecting 2 points on the sphere is a __________. If a plane intersects a sphere, the intersection is a __________. If the circle’s center is the center o ...
... SA & V of Spheres Definition of a sphere: The distance from the center to the sphere is called the __________. A segment passing thru the center connecting 2 points on the sphere is a __________. If a plane intersects a sphere, the intersection is a __________. If the circle’s center is the center o ...
229 ACTION OF GENERALIZED LIE GROUPS ON
... group is the set of transformations acting on the M inkowski spacetime. To study more general cases, the notion of top spaces as a generalization of Lie groups was introduced by M. R. Molaei in 1998 [3]. Here we would like to study the action of a top space T on a manifold M . Moreover we have encou ...
... group is the set of transformations acting on the M inkowski spacetime. To study more general cases, the notion of top spaces as a generalization of Lie groups was introduced by M. R. Molaei in 1998 [3]. Here we would like to study the action of a top space T on a manifold M . Moreover we have encou ...
fragmentability by the discrete metric
... Theorem 5 [21, Theorem 1.2]. Let τ1 , τ2 be two (not necessarily distinct) topologies on a set X. The space (X, τ1 ) is fragmentable by a metric whose topology is at least as strong as τ2 if, and only if, the player B has a winning strategy in the G (X, τ1 , τ2 )-game played on X. Throughout the rem ...
... Theorem 5 [21, Theorem 1.2]. Let τ1 , τ2 be two (not necessarily distinct) topologies on a set X. The space (X, τ1 ) is fragmentable by a metric whose topology is at least as strong as τ2 if, and only if, the player B has a winning strategy in the G (X, τ1 , τ2 )-game played on X. Throughout the rem ...
A GENERALLY COVARIANT FIELD EQUATION FOR GRAVITATION
... Equation (43) shows that for both gravitation and electromagnetism the generally covariant energy momentum four-vector T µ is proportional to the generally covariant metric four-vector q µ through the metric dependent proportionality coefficient α. It is likely that such a result is also true for th ...
... Equation (43) shows that for both gravitation and electromagnetism the generally covariant energy momentum four-vector T µ is proportional to the generally covariant metric four-vector q µ through the metric dependent proportionality coefficient α. It is likely that such a result is also true for th ...
9/21 handout
... 1. In any discrete space, each singleton {x} is open, and in order for a sequence (xn ) to converge to x, (xn ) must be eventually in {x}, which means (xn ) must be eventually constant. 2. In any indiscrete space (X, τi ), every sequence τi -converges to every point. Remark: These first two examples ...
... 1. In any discrete space, each singleton {x} is open, and in order for a sequence (xn ) to converge to x, (xn ) must be eventually in {x}, which means (xn ) must be eventually constant. 2. In any indiscrete space (X, τi ), every sequence τi -converges to every point. Remark: These first two examples ...