MI314 – History of Mathematics: Introduction to proofs
... A proof of existence, by construction, Theodosius Spherics II 6 Definitions. In sphere, a great circle is a circle whose plane passes through the center of the sphere, an a lesser circle is any other circle. Lesser circles form bundles of parallels sharing the same two poles. The pole-distance of a c ...
... A proof of existence, by construction, Theodosius Spherics II 6 Definitions. In sphere, a great circle is a circle whose plane passes through the center of the sphere, an a lesser circle is any other circle. Lesser circles form bundles of parallels sharing the same two poles. The pole-distance of a c ...
Poincaré`s Disk Model for Hyperbolic Geometry
... must have to make some major changes in our concept of point, line, and/or distance. We need a model to see what H 2 looks like. We know that it will not be easy, but we do not want some extremely difficult model to construct. We will work with a small subset of the plane, but give it a different wa ...
... must have to make some major changes in our concept of point, line, and/or distance. We need a model to see what H 2 looks like. We know that it will not be easy, but we do not want some extremely difficult model to construct. We will work with a small subset of the plane, but give it a different wa ...
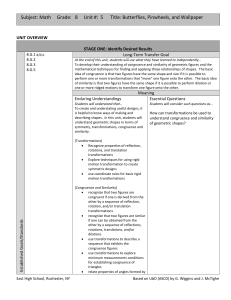
Geometry bridging document sem 1 09092013
... Similarity, Right Triangles, and Trigonometry Understand similarity in terms of similarity transformations. 1.Verify experimentally the properties of dilations given by a center and a scale factor: a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leav ...
... Similarity, Right Triangles, and Trigonometry Understand similarity in terms of similarity transformations. 1.Verify experimentally the properties of dilations given by a center and a scale factor: a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leav ...
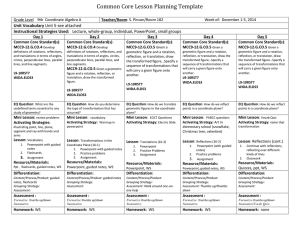
Common Core Lesson Planning Template
... • Isometry: a distance preserving map of a geometric figure to another location using a reflection, rotation or translation. Indicates an isometry of the figure M to a new location M’. M and M’ remain congruent. • Line: One of the undefined terms of geometry that represents an infinite set of points ...
... • Isometry: a distance preserving map of a geometric figure to another location using a reflection, rotation or translation. Indicates an isometry of the figure M to a new location M’. M and M’ remain congruent. • Line: One of the undefined terms of geometry that represents an infinite set of points ...
Strange Geometries
... thought geometry should be built. One of them, the fifth, was equivalent to a statement we are all familiar with: that the angles in a triangle add up to 180 degrees. However, this postulate did not seem as obvious as the other four on Euclid’s list, so mathematicians attempted to deduce it from the ...
... thought geometry should be built. One of them, the fifth, was equivalent to a statement we are all familiar with: that the angles in a triangle add up to 180 degrees. However, this postulate did not seem as obvious as the other four on Euclid’s list, so mathematicians attempted to deduce it from the ...
Geometry - Perfection Learning
... following: opposite sides are congruent; opposite angles are congruent; the diagonals of a parallelogram bisect each other; and rectangles are parallelograms with congruent diagonals. Prove that given quadrilaterals are parallelograms, rhombuses, rectangles, squares or trapezoids. Include coordinate ...
... following: opposite sides are congruent; opposite angles are congruent; the diagonals of a parallelogram bisect each other; and rectangles are parallelograms with congruent diagonals. Prove that given quadrilaterals are parallelograms, rhombuses, rectangles, squares or trapezoids. Include coordinate ...
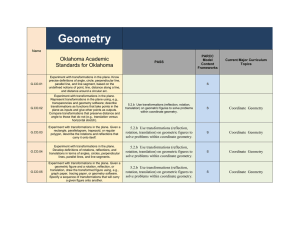
Priority Standards Checklist Priority Standard Geometry PRIORITY
... G-CO.13 Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle. G-SRT.1 Verify experimentally the properties of dilations given by a center and a scale factor: a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves ...
... G-CO.13 Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle. G-SRT.1 Verify experimentally the properties of dilations given by a center and a scale factor: a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves ...
HOMEWORK ASSIGNMENT #6 SOLUTIONS
... There exist three non-collinear points through which no circle passes. 2. (Exercise 9.2.4, page 374) Without using an axiom of parallelism, prove that if a transversal of two lines makes the alternate angles congruent, then the two given lines do not intersect. Let m and n be the two lines cut by th ...
... There exist three non-collinear points through which no circle passes. 2. (Exercise 9.2.4, page 374) Without using an axiom of parallelism, prove that if a transversal of two lines makes the alternate angles congruent, then the two given lines do not intersect. Let m and n be the two lines cut by th ...
Geometry - BAschools.org
... three-dimensional objects. Identify the shapes of twodimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects. ...
... three-dimensional objects. Identify the shapes of twodimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects. ...
LOGIC AND INCIDENCE GEOMETRY
... most obvious. Although it is "obvious" that two points determine a unique line, Euclid stated this as his first postulate. So ifin some proof we want to say that every line has points lying on it, we should list this statement as another postulate (or prove it. but we can't). In other words, all our ...
... most obvious. Although it is "obvious" that two points determine a unique line, Euclid stated this as his first postulate. So ifin some proof we want to say that every line has points lying on it, we should list this statement as another postulate (or prove it. but we can't). In other words, all our ...
GEOMETRY LTs 16-17
... (G-GPE.5) - Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point). (G-GPE.6) - Find the point on a directed line segment between two given ...
... (G-GPE.5) - Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point). (G-GPE.6) - Find the point on a directed line segment between two given ...
TN Geometry Traditional Pacing Guide 2017-18
... scale factor: A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. ...
... scale factor: A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. The dilation of a line segment is longer or shorter in the ratio given by the scale factor. ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.