An Introduction to Non-Euclidean Geometry
... Euclid’s Elements Euclid’s Propositions The 48 propositions are accompanied by a proof using the common notions, postulates, and previous propositions. The 29th proposition states: A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle ...
... Euclid’s Elements Euclid’s Propositions The 48 propositions are accompanied by a proof using the common notions, postulates, and previous propositions. The 29th proposition states: A straight line falling on parallel straight lines makes the alternate angles equal to one another, the exterior angle ...
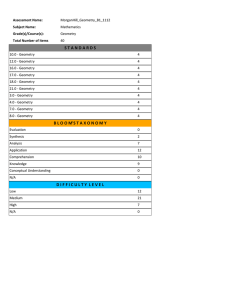
Geometry 1
... Geometry - 18.0 - Geometry - Students know the definitions of the basic trigonometric functions defined by the angles of a right triangle. They also know and are able to use elementary relationships between them. For example, tan(x) = sin(x)/cos(x), (sin(x))² + (cos(x))² = 1. ...
... Geometry - 18.0 - Geometry - Students know the definitions of the basic trigonometric functions defined by the angles of a right triangle. They also know and are able to use elementary relationships between them. For example, tan(x) = sin(x)/cos(x), (sin(x))² + (cos(x))² = 1. ...
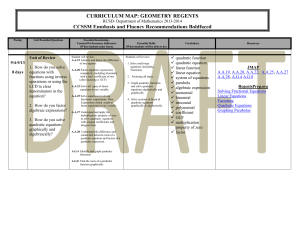
Pacing
... paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another. Prove geometric theorems ...
... paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another. Prove geometric theorems ...
File
... State the CPCTC Theorem DESCRIBE how Triangle Congruence is Reflexive, Symmetric and Transitive Use CPCTC in a Proof ...
... State the CPCTC Theorem DESCRIBE how Triangle Congruence is Reflexive, Symmetric and Transitive Use CPCTC in a Proof ...
Compact hyperbolic tetrahedra with non
... The first step is to make sure that the dihedral angles of a compact tetrahedron satisfy conditions (1-3). For condition (1), notice that if two adjacent faces intersect along a line segment with dihedral angle 0, they would coincide. In addition, the dihedral angle between adjacent faces is ≤ π/2 b ...
... The first step is to make sure that the dihedral angles of a compact tetrahedron satisfy conditions (1-3). For condition (1), notice that if two adjacent faces intersect along a line segment with dihedral angle 0, they would coincide. In addition, the dihedral angle between adjacent faces is ≤ π/2 b ...
Saccheri and Lambert quadrilateral in Hyperbolic Geometry.
... diameter of the disk. (Do this as closely as you can. It is not mathematically significant that this segment lies on the diameter, but let us do this for our first picture.) 2. Use Constructions → Draw Perpendicular. Click on AB then point A to draw a perpendicular line at point A. 3. Use Constructi ...
... diameter of the disk. (Do this as closely as you can. It is not mathematically significant that this segment lies on the diameter, but let us do this for our first picture.) 2. Use Constructions → Draw Perpendicular. Click on AB then point A to draw a perpendicular line at point A. 3. Use Constructi ...
geometry - Calculate
... • acute (less than 900) • right angle (exactly 900) • obtuse (between 900 and 1800) • straight (exactly 1800) • reflex (more than 1800) ...
... • acute (less than 900) • right angle (exactly 900) • obtuse (between 900 and 1800) • straight (exactly 1800) • reflex (more than 1800) ...
The Parallel Postulate is Depended on the Other Axioms
... only, therefore the great circles are not lines (this is because it is MA + MA΄ > AA΄) and the curvature of Space is that of the circle in this Plane, i.e. that of the circle (O, OA), which are more than three points. Because Parallel Axiom is for three points only, which consist a Plane, then the c ...
... only, therefore the great circles are not lines (this is because it is MA + MA΄ > AA΄) and the curvature of Space is that of the circle in this Plane, i.e. that of the circle (O, OA), which are more than three points. Because Parallel Axiom is for three points only, which consist a Plane, then the c ...
Coordinate Geometry
... of the angle, and the lines ___(2)____(call) the sides or rays of the angle. Angles ____(3)___(be) usually measured in degrees. Two angles are adjacent if they have the same vertex and a common side, and one angle _____(4)___(be) not inside the other. If two lines intersect at a point, they form fou ...
... of the angle, and the lines ___(2)____(call) the sides or rays of the angle. Angles ____(3)___(be) usually measured in degrees. Two angles are adjacent if they have the same vertex and a common side, and one angle _____(4)___(be) not inside the other. If two lines intersect at a point, they form fou ...
Old and New Results in the Foundations of Elementary Plane
... For arbitrary Hilbert planes, the Circle-Circle axiom is equivalent to the Triangle Existence theorem [20, Corollary, p. 173] and implies the Line-Circle axiom [20, Major Exercise 1, p. 200]. Conversely, Strommer [43] proved that Line-Circle implies Circle-Circle in all Hilbert planes, first proving ...
... For arbitrary Hilbert planes, the Circle-Circle axiom is equivalent to the Triangle Existence theorem [20, Corollary, p. 173] and implies the Line-Circle axiom [20, Major Exercise 1, p. 200]. Conversely, Strommer [43] proved that Line-Circle implies Circle-Circle in all Hilbert planes, first proving ...
Slides for Nov. 12, 2014, lecture
... number of magnitude-concepts, each of which must be specified according to its mode in order to individuate and identify an instance of that concept; ordinary physical space, e.g., is a triply extended magnitude, because it needs three spatial lengths (coordinates, say, in a fixed coordinate system) ...
... number of magnitude-concepts, each of which must be specified according to its mode in order to individuate and identify an instance of that concept; ordinary physical space, e.g., is a triply extended magnitude, because it needs three spatial lengths (coordinates, say, in a fixed coordinate system) ...
optimal angle bounds for quadrilateral meshes
... a linear time algorithm for finding the mesh, the constant is large and the construction depends on other linear algorithms, such Chazelle’s linear time triangulation of polygons, that have not been implemented (as far as I know). The three main tools in the proof of Theorem 1.1 are conformal maps, ...
... a linear time algorithm for finding the mesh, the constant is large and the construction depends on other linear algorithms, such Chazelle’s linear time triangulation of polygons, that have not been implemented (as far as I know). The three main tools in the proof of Theorem 1.1 are conformal maps, ...
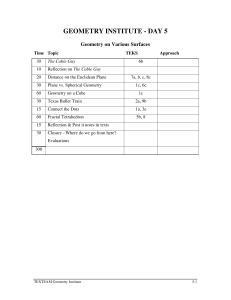
geometry institute - day 5
... ∠2, nor change the length of AC and BC, the shortest path between A and B is the one shown in figure 1. It can be described geometrically as the unbroken path formed by straight lines on each face that meet the common edge in supplementary angles. When, as in figure 3, A and B do not lie on adjacent ...
... ∠2, nor change the length of AC and BC, the shortest path between A and B is the one shown in figure 1. It can be described geometrically as the unbroken path formed by straight lines on each face that meet the common edge in supplementary angles. When, as in figure 3, A and B do not lie on adjacent ...
The parallel postulate, the other four and Relativity
... = π. AB ², i.e. one square equal to the area of the unit circle. Four points A,B,C,D (....) not coinciding, consist a new Unit (the Space or Space Layer) without position also, which is extended between the four Planes and all included, forming Volume ABCD and since is composed of infinite Planes wh ...
... = π. AB ², i.e. one square equal to the area of the unit circle. Four points A,B,C,D (....) not coinciding, consist a new Unit (the Space or Space Layer) without position also, which is extended between the four Planes and all included, forming Volume ABCD and since is composed of infinite Planes wh ...
answer key
... feet. Gloria thinks that this rug will need half as much braid as the circular rug. Explain why Gloria is not correct. How much braid will this rug need? Sample Response Gloria is incorrect because although you need half of the braid of the circular ring, you also need to account for the addition st ...
... feet. Gloria thinks that this rug will need half as much braid as the circular rug. Explain why Gloria is not correct. How much braid will this rug need? Sample Response Gloria is incorrect because although you need half of the braid of the circular ring, you also need to account for the addition st ...
A Brief Survey of Elliptic Geometry
... “point” is defined as a pair of antipodal points and a “line” is defined as a great circle of the sphere. This model may sound deceptively simple at first glance, but since this model has no parallel lines, it is not a model of neutral geometry. See Chapter 2 Section I for an overview of the axioms ...
... “point” is defined as a pair of antipodal points and a “line” is defined as a great circle of the sphere. This model may sound deceptively simple at first glance, but since this model has no parallel lines, it is not a model of neutral geometry. See Chapter 2 Section I for an overview of the axioms ...
Geometry Fall Semester Final Review
... Find the range for the measure of the third side of a triangle given the measures of two sides. 7. 25 yd and 38 yd ...
... Find the range for the measure of the third side of a triangle given the measures of two sides. 7. 25 yd and 38 yd ...
What is Hyperbolic Geometry? - School of Mathematics, TIFR
... In the 18th century, Johann Heinrich Lambert introduced what are today called hyperbolic functions and computed the area of a hyperbolic triangle. In the nineteenth century, hyperbolic geometry was extensively explored by the Hungarian mathematician Janos Bolyai and the Russian mathematician Nikolai ...
... In the 18th century, Johann Heinrich Lambert introduced what are today called hyperbolic functions and computed the area of a hyperbolic triangle. In the nineteenth century, hyperbolic geometry was extensively explored by the Hungarian mathematician Janos Bolyai and the Russian mathematician Nikolai ...
What is Hyperbolic Geometry?
... In the 18th century, Johann Heinrich Lambert introduced what are today called hyperbolic functions and computed the area of a hyperbolic triangle. In the nineteenth century, hyperbolic geometry was extensively explored by the Hungarian mathematician Janos Bolyai and the Russian mathematician Nikolai ...
... In the 18th century, Johann Heinrich Lambert introduced what are today called hyperbolic functions and computed the area of a hyperbolic triangle. In the nineteenth century, hyperbolic geometry was extensively explored by the Hungarian mathematician Janos Bolyai and the Russian mathematician Nikolai ...
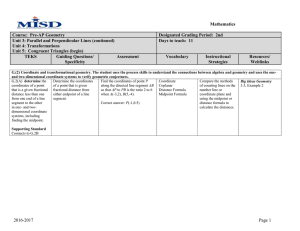
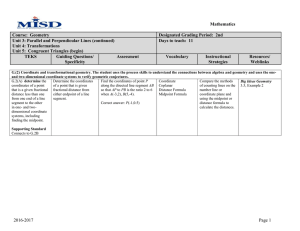
2nd Unit 3: Parallel and Perpendicular Lines
... G.(2) Coordinate and transformational geometry. The student uses the process skills to understand the connections between algebra and geometry and uses the oneand two-dimensional coordinate systems to verify geometric conjectures. G.2(A) determine the Determine the coordinates Find the coordinates o ...
... G.(2) Coordinate and transformational geometry. The student uses the process skills to understand the connections between algebra and geometry and uses the oneand two-dimensional coordinate systems to verify geometric conjectures. G.2(A) determine the Determine the coordinates Find the coordinates o ...
RATIONAL ANGLED HYPERBOLIC POLYGONS 1
... polygons with algebraic side lengths. Throughout, H2 denotes the hyperbolic plane of constant Gaussian curvature K = −1. We adopt Poincaré’s conformal disk model of H2 for our figures. Below, we prove that every rational angled hyperbolic triangle has transcendental side lengths and every rational a ...
... polygons with algebraic side lengths. Throughout, H2 denotes the hyperbolic plane of constant Gaussian curvature K = −1. We adopt Poincaré’s conformal disk model of H2 for our figures. Below, we prove that every rational angled hyperbolic triangle has transcendental side lengths and every rational a ...
Chapter 4
... There isn’t anything special about which two angles we’re talking about, so clearly, any pair of angles from this triangle must sum to less than 180◦ . As a look ahead, note that in Figure 5, AC and BF are parallel and congruent. Therefore, 4ABC and 4ABF have the same base and the same height. The a ...
... There isn’t anything special about which two angles we’re talking about, so clearly, any pair of angles from this triangle must sum to less than 180◦ . As a look ahead, note that in Figure 5, AC and BF are parallel and congruent. Therefore, 4ABC and 4ABF have the same base and the same height. The a ...
2.7.1 Euclidean Parallel Postulate
... Euclid's Fifth Postulate. That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. SMSG Postulate 16. (Eucli ...
... Euclid's Fifth Postulate. That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles. SMSG Postulate 16. (Eucli ...
2nd Unit 3: Parallel and Perpendicular Lines
... G.(2) Coordinate and transformational geometry. The student uses the process skills to understand the connections between algebra and geometry and uses the oneand two-dimensional coordinate systems to verify geometric conjectures. G.2(A) determine the Determine the coordinates Find the coordinates o ...
... G.(2) Coordinate and transformational geometry. The student uses the process skills to understand the connections between algebra and geometry and uses the oneand two-dimensional coordinate systems to verify geometric conjectures. G.2(A) determine the Determine the coordinates Find the coordinates o ...
Hyperbolic geometry
In mathematics, hyperbolic geometry (also called Bolyai–Lobachevskian geometry or Lobachevskian geometry) is a non-Euclidean geometry. In hyperbolic geometry the parallel postulate of Euclidean geometry is replaced with:For any given line R and point P not on R, in the plane containing both line R and point P there are at least two distinct lines through P that do not intersect R.(compare this with Playfair's axiom the modern version of Euclid's parallel postulate)Hyperbolic plane geometry is also the geometry of saddle surface or pseudospherical surfaces, surfaces with a constant negative Gaussian curvature.A modern use of hyperbolic geometry is in the theory of special relativity, particularly Minkowski spacetime and gyrovector space.When geometers first realised they worked with something else than the standard Euclidean geometry they described their geometry under many different names; Felix Klein finally gave the subject the name hyperbolic geometry. It was for putting it in the now rarely used sequence elliptic geometry (spherical geometry) , parabolic geometry (Euclidean geometry), and hyperbolic geometry.In Russia it is commonly called Lobachevskian geometry after one of its discoverers, the Russian geometer Nikolai Lobachevsky.This page is mainly about the 2 dimensional or plane hyperbolic geometry and the differences and similarities between Euclidean and hyperbolic geometry.Hyperbolic geometry can be extended to three and more dimensions; see hyperbolic space for more on the three and higher dimensional cases.