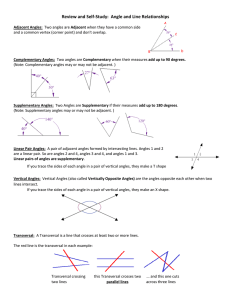
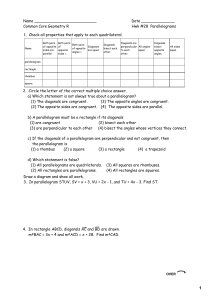
Understand Angle Relationships Vocabulary
... Find the measure of EBF. ABC and DBF are vertical angles, so they have the same measure. Because m ABC is 90°, the sum of m DBE and m EBF must also be 90°. Solve for x in this equation. ...
... Find the measure of EBF. ABC and DBF are vertical angles, so they have the same measure. Because m ABC is 90°, the sum of m DBE and m EBF must also be 90°. Solve for x in this equation. ...
What is an Angle
... We can specify an angle by using a point on each ray and the vertex. The angle below may be specified as angle ABC or as angle CBA; you may also see this written as ABC or as CBA. Note how the vertex point is always given in the middle. ...
... We can specify an angle by using a point on each ray and the vertex. The angle below may be specified as angle ABC or as angle CBA; you may also see this written as ABC or as CBA. Note how the vertex point is always given in the middle. ...
Vertical Angles
... *Vertex – the “corner” of the angle *Ray – a line that has an endpoint on one end and goes on forever in the other direction. ...
... *Vertex – the “corner” of the angle *Ray – a line that has an endpoint on one end and goes on forever in the other direction. ...
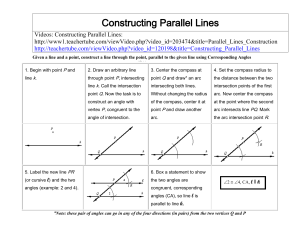
Constructing Parallel Lines
... four by constructing congruent angles for each pair of Alternate Interior Angles (AIA's) - doing both the obtuse and acute angles (two times each). Make two by constructing supplementary angles for each pair of Same Side Interior Angles (SSIA's). Make two more by constructing a perpendicular transve ...
... four by constructing congruent angles for each pair of Alternate Interior Angles (AIA's) - doing both the obtuse and acute angles (two times each). Make two by constructing supplementary angles for each pair of Same Side Interior Angles (SSIA's). Make two more by constructing a perpendicular transve ...
The parallel postulate, the other four and Relativity
... side A1M΄ = B1M (Cn1). Triangles A1MM΄,B1M΄M are equal because have the three sides equal each other, therefore angle < A1MM΄ = B1M΄M, and since their sum is 180▫ as before (6D), so angle < A1MM΄ = B1M΄M = 90▫ (Cn2). d. Since angle < A1MM΄ = A1CC΄ and also angle < B1M΄M = B1CC΄ (P4), therefore quadr ...
... side A1M΄ = B1M (Cn1). Triangles A1MM΄,B1M΄M are equal because have the three sides equal each other, therefore angle < A1MM΄ = B1M΄M, and since their sum is 180▫ as before (6D), so angle < A1MM΄ = B1M΄M = 90▫ (Cn2). d. Since angle < A1MM΄ = A1CC΄ and also angle < B1M΄M = B1CC΄ (P4), therefore quadr ...
Lesson Plan Format
... All __________ are congruent in an equilateral polygon. All __________ are congruent in an equiangular polygon. A _______________ polygon is one that is both equilateral and equiangular. If a polygon is not regular, it is called irregular. A polygon is __________ if it has one or more interior angl ...
... All __________ are congruent in an equilateral polygon. All __________ are congruent in an equiangular polygon. A _______________ polygon is one that is both equilateral and equiangular. If a polygon is not regular, it is called irregular. A polygon is __________ if it has one or more interior angl ...