Geometry Unit 1 Introducing Line, Angle, Triangle and Parallelogram
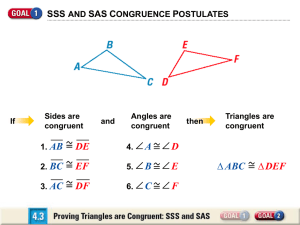
... A triangle is a shape made up of three line segments or three sides. A triangle has three points, one at each corner. At each point there is an angle. To compare triangles we always compare the length of the sides and the size of each of the angles. ...
... A triangle is a shape made up of three line segments or three sides. A triangle has three points, one at each corner. At each point there is an angle. To compare triangles we always compare the length of the sides and the size of each of the angles. ...
List all pairs of congruent angles for the figures
... List all pairs of congruent angles for the figures. Then write the ratios of the corresponding sides in a statement of proportionality. ...
... List all pairs of congruent angles for the figures. Then write the ratios of the corresponding sides in a statement of proportionality. ...
Name
... Name: ______________________ Date: ___________ Period: _____ Homework 9.4 Geometry’s Most Elegant Theorem ...
... Name: ______________________ Date: ___________ Period: _____ Homework 9.4 Geometry’s Most Elegant Theorem ...