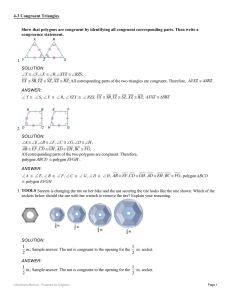
Section 2.6 Special Angles on Parallel Lines Notes
... Definitions from this section: transversal, corresponding angles, alternate interior angles, alternate exterior angles, same side interior angles, parallel lines conjecture. Homework: Review p. 128 - 131 and Do p. 131-134 #1-7, 9, 14-16, 19, 20 plus study for the quiz on Section 2.1 and 2.4 Warm up: ...
... Definitions from this section: transversal, corresponding angles, alternate interior angles, alternate exterior angles, same side interior angles, parallel lines conjecture. Homework: Review p. 128 - 131 and Do p. 131-134 #1-7, 9, 14-16, 19, 20 plus study for the quiz on Section 2.1 and 2.4 Warm up: ...
Chapter 3.angles
... 1. The point that the two rays intersect is called the ________________________. 2. The two rays are called the ______________ of the angle. 3. When naming angles, it is typical to use one or three letters. Sometimes one cannot use one letter. When using three letters, the _________________ must be ...
... 1. The point that the two rays intersect is called the ________________________. 2. The two rays are called the ______________ of the angle. 3. When naming angles, it is typical to use one or three letters. Sometimes one cannot use one letter. When using three letters, the _________________ must be ...
geometry 1a 1st semester review
... B If alternate interior angles are congruent, then the lines are parallel. C If vertical angles are congruent, then the lines are parallel. D If alternate exterior angles are congruent, then the lines are parallel. ...
... B If alternate interior angles are congruent, then the lines are parallel. C If vertical angles are congruent, then the lines are parallel. D If alternate exterior angles are congruent, then the lines are parallel. ...
GETE0305
... You can draw exterior angles at any vertex of a polygon. The figures below show that the sum of the measures of the exterior angles, one at each vertex, is 360. This can be proved as a theorem in a way suggested in Exercise 46. ...
... You can draw exterior angles at any vertex of a polygon. The figures below show that the sum of the measures of the exterior angles, one at each vertex, is 360. This can be proved as a theorem in a way suggested in Exercise 46. ...
Lecture
... simply state the steps in paragraph form. Another method is to lay it out just as you do when solving an algebra equation. Either way is acceptable. I prefer the line-by-line method as for me it is easier to follow each step. Here we go…let’s prove our conjecture. First, let’s plan out our strategy. ...
... simply state the steps in paragraph form. Another method is to lay it out just as you do when solving an algebra equation. Either way is acceptable. I prefer the line-by-line method as for me it is easier to follow each step. Here we go…let’s prove our conjecture. First, let’s plan out our strategy. ...
2205 Unit 1 NOTES - North Penn School District
... Look for a pattern. What are the next three terms in each sequence? ...
... Look for a pattern. What are the next three terms in each sequence? ...