Chapter 7 Study Guide Name: ____________ Geometry Target 7.1
... 18) John, who is 5 ft. 9 in. tall, wanted to know the height of the MacDonald’s sign. At the same time of day, he measured his shadow and the sign’s shadow. He found that his shadow was 7 ft. 8 in. and the the sign’s shadow was 38 ft. 4 in. shadow. What is the height of the sign in inches? In feet? ...
... 18) John, who is 5 ft. 9 in. tall, wanted to know the height of the MacDonald’s sign. At the same time of day, he measured his shadow and the sign’s shadow. He found that his shadow was 7 ft. 8 in. and the the sign’s shadow was 38 ft. 4 in. shadow. What is the height of the sign in inches? In feet? ...
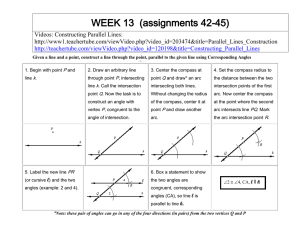
Parallel Lines
... By the end of the unit, I will…. » Be able to identify different types of angles and lines. » Use arguments to establish facts about angle sums and exterior angles of triangles. » Identify the angles created when parallel lines are cut by a transversal. » Create arguments for the similarity of trian ...
... By the end of the unit, I will…. » Be able to identify different types of angles and lines. » Use arguments to establish facts about angle sums and exterior angles of triangles. » Identify the angles created when parallel lines are cut by a transversal. » Create arguments for the similarity of trian ...
8.7 Extension: Laws of Sines and Cosines
... know about these ratios and derive the Law of Sines and the Law of Cosines. Both of these laws can be used with any type of triangle to find any angle or side within it. That means we can find the sine, cosine and tangent of angle that are greater than 90◦ , such as the obtuse angle in an obtuse tri ...
... know about these ratios and derive the Law of Sines and the Law of Cosines. Both of these laws can be used with any type of triangle to find any angle or side within it. That means we can find the sine, cosine and tangent of angle that are greater than 90◦ , such as the obtuse angle in an obtuse tri ...
angle
... Adjacent Angles • Adjacent angles – two angles that lie in the same plane, have a common vertex, and share a common side, but NO common interior points. C A ...
... Adjacent Angles • Adjacent angles – two angles that lie in the same plane, have a common vertex, and share a common side, but NO common interior points. C A ...