DG U2 D12 N4 Finding Congruent Triangles.2015-16
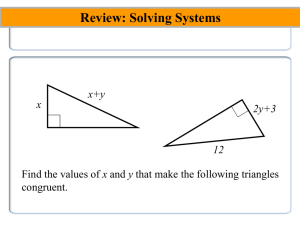
... ____ Side is congruent to itself ( a shared side between two triangles) ____ Definition of a midpoint ( a midpoint bisects a segment ...
... ____ Side is congruent to itself ( a shared side between two triangles) ____ Definition of a midpoint ( a midpoint bisects a segment ...
Chapter 5
... Theorem, which relates the sides of a right triangle, we can find the distance between two points. Definition The Pythagorean Theorem states that the sum of the squares of the legs of a right triangle will equal the square of the hypotenuse of the triangle. In graphical form, given the triangle show ...
... Theorem, which relates the sides of a right triangle, we can find the distance between two points. Definition The Pythagorean Theorem states that the sum of the squares of the legs of a right triangle will equal the square of the hypotenuse of the triangle. In graphical form, given the triangle show ...
Geometry Mathematics Curriculum Guide
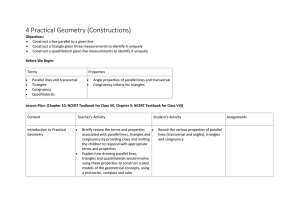
... Describe and apply the different types of transformations and be able to differentiate between them Perform translations, reflections, and rotations with and without the use of technology; including reflecting over parallel lines and reflecting over intersecting lines Describe and perform the compos ...
... Describe and apply the different types of transformations and be able to differentiate between them Perform translations, reflections, and rotations with and without the use of technology; including reflecting over parallel lines and reflecting over intersecting lines Describe and perform the compos ...
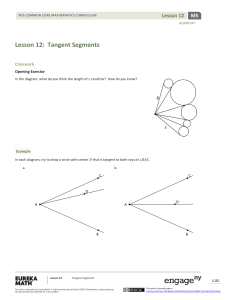
Lesson 13: The Inscribed Angle Alternate—A Tangent Angle
... We have shown that the inscribed angle theorem can be extended to the case when one of the angle’s rays is a tangent segment and the vertex is the point of tangency. The Example develops another theorem in the inscribed angle theorem’s family: the angle formed by the intersection of the tangent line ...
... We have shown that the inscribed angle theorem can be extended to the case when one of the angle’s rays is a tangent segment and the vertex is the point of tangency. The Example develops another theorem in the inscribed angle theorem’s family: the angle formed by the intersection of the tangent line ...