An Angle on Geometry
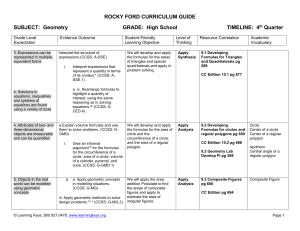
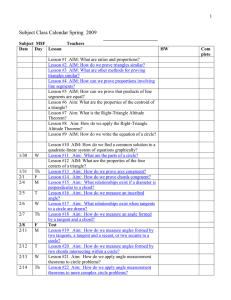
... Angles in a wide range of 2D objects are explored, specifically, the angles of scalene, isosceles and equilateral triangles, parallel and intersecting lines and angles in a circle. In addition, there are several pages that apply many of these concepts to angles in everyday situations. The book also ...
... Angles in a wide range of 2D objects are explored, specifically, the angles of scalene, isosceles and equilateral triangles, parallel and intersecting lines and angles in a circle. In addition, there are several pages that apply many of these concepts to angles in everyday situations. The book also ...
Geometry and Measurement of Plane Figures Activity Set 3 Trainer
... • Demonstrate how to create a proportional grid by drawing a new box below the existing image. Make it with a scale factor of 2 : 1. The new box will be twice as wide and twice as tall. • Point out a small section of the image and sketch the part contained in the section into the corresponding secti ...
... • Demonstrate how to create a proportional grid by drawing a new box below the existing image. Make it with a scale factor of 2 : 1. The new box will be twice as wide and twice as tall. • Point out a small section of the image and sketch the part contained in the section into the corresponding secti ...
polygon - DArmitage
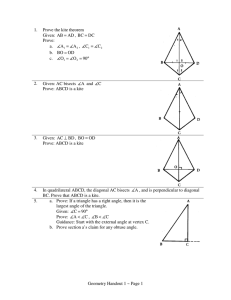
... segments. A regular polygon is a polygon in which all sides are congruent and all angles are congruent. Polygons are named by the number of their sides and angles. Course 1 ...
... segments. A regular polygon is a polygon in which all sides are congruent and all angles are congruent. Polygons are named by the number of their sides and angles. Course 1 ...
Foundations of Geometry
... The material contained in the following translation was given in substance by Professor Hilbert as a course of lectures on euclidean geometry at the University of Göttingen during the winter semester of 1898–1899. The results of his investigation were re-arranged and put into the form in which they ...
... The material contained in the following translation was given in substance by Professor Hilbert as a course of lectures on euclidean geometry at the University of Göttingen during the winter semester of 1898–1899. The results of his investigation were re-arranged and put into the form in which they ...