EUCLIDEAN GEOMETRY Contents 1. Euclid`s geometry as a theory
... other words, if we can move a figure (angle or segment) to fit exactly on top of the other, then it means they are equal (in terms of size). 5) The whole is greater than the part. In other words, we can show an object to be smaller than another object by moving the smaller object until it fits insid ...
... other words, if we can move a figure (angle or segment) to fit exactly on top of the other, then it means they are equal (in terms of size). 5) The whole is greater than the part. In other words, we can show an object to be smaller than another object by moving the smaller object until it fits insid ...
MTH 362: Study Guide for the Exam 2
... c. Q3: Are the diagonals bisecting each other? d. Q4: Diagonals split the rhombus into 4 triangles. They all share certain properties. Name and justify at least one such property. e. Prove that a rhombus is a parallelogram. Use only triangle congruence theorems, Isosceles Triangle Theorem and theore ...
... c. Q3: Are the diagonals bisecting each other? d. Q4: Diagonals split the rhombus into 4 triangles. They all share certain properties. Name and justify at least one such property. e. Prove that a rhombus is a parallelogram. Use only triangle congruence theorems, Isosceles Triangle Theorem and theore ...
Proofs - Net Start Class
... a. The opposite angles of an inscribed quadrilateral are congruent. b. The opposite angles of an inscribed quadrilateral are right angles. c. The opposite angles of an inscribed quadrilateral are complementary. d. The opposite angles of an inscribed quadrilateral are supplementary. ...
... a. The opposite angles of an inscribed quadrilateral are congruent. b. The opposite angles of an inscribed quadrilateral are right angles. c. The opposite angles of an inscribed quadrilateral are complementary. d. The opposite angles of an inscribed quadrilateral are supplementary. ...
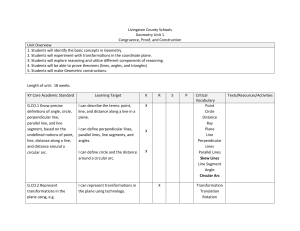
Livingston County Schools Geometry Unit 1 Congruence, Proof, and
... 1. Students will identify the basic concepts in Geometry. 2. Students will experiment with transformations in the coordinate plane. 3. Students will explore reasoning and utilize different components of reasoning. 4. Students will be able to prove theorems (lines, angles, and triangles) ...
... 1. Students will identify the basic concepts in Geometry. 2. Students will experiment with transformations in the coordinate plane. 3. Students will explore reasoning and utilize different components of reasoning. 4. Students will be able to prove theorems (lines, angles, and triangles) ...