Proof - USD 343
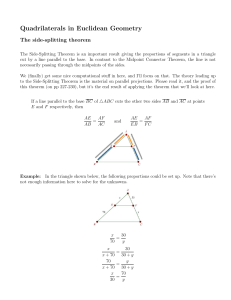
... Since E is the midpoint of AB by the Midpoint Theorem we know that AE EB, similarly we know that CE ED. By the definition of congruent segments we know that AE = EB = ½ AB, similarly we also know that CE = ED = ½ CD. Since we know that AB = CD, by the multiplication property we can say that ½ AB ...
... Since E is the midpoint of AB by the Midpoint Theorem we know that AE EB, similarly we know that CE ED. By the definition of congruent segments we know that AE = EB = ½ AB, similarly we also know that CE = ED = ½ CD. Since we know that AB = CD, by the multiplication property we can say that ½ AB ...
Holt McDougal Geometry 8-3
... Using given measures to find the unknown angle measures or side lengths of a triangle is known as solving a triangle. To solve a right triangle, you need to know two side lengths or one side length and an acute angle measure. ...
... Using given measures to find the unknown angle measures or side lengths of a triangle is known as solving a triangle. To solve a right triangle, you need to know two side lengths or one side length and an acute angle measure. ...
CHAPTER
... 7. What is the sum of the measures of the interior angles of a regular 72-gon? A 6480 ...
... 7. What is the sum of the measures of the interior angles of a regular 72-gon? A 6480 ...
Geometry
... and write proofs of theorems and other results in geometry, including proofs by contradiction. Express proofs in a form that clearly justifies the reasoning, such as twocolumn proofs, paragraph proofs, flow charts or illustrations Know and apply properties of parallel and perpendicular lines, includ ...
... and write proofs of theorems and other results in geometry, including proofs by contradiction. Express proofs in a form that clearly justifies the reasoning, such as twocolumn proofs, paragraph proofs, flow charts or illustrations Know and apply properties of parallel and perpendicular lines, includ ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)