7-5 notes (Word)
... Theorem 7-1 – SAS Similarity Theorem – If an angle of one triangle is congruent to an angle of another triangle and the sides including those angles are in proportion, then the triangles are similar D A ...
... Theorem 7-1 – SAS Similarity Theorem – If an angle of one triangle is congruent to an angle of another triangle and the sides including those angles are in proportion, then the triangles are similar D A ...
Similar Triangles
... • Triangles are similar if they have the same shape, but not necessarily the same size • These triangles are all similar: ...
... • Triangles are similar if they have the same shape, but not necessarily the same size • These triangles are all similar: ...
and Measurement
... like rectangles; possibly more than one set Congruent – of equal measure, having exactly the same size and same shape Equation – a mathematical statement composed of algebraic and/or numeric expressions set equal to each other Face – a flat surface of a three-dimensional figure Height of a rectangul ...
... like rectangles; possibly more than one set Congruent – of equal measure, having exactly the same size and same shape Equation – a mathematical statement composed of algebraic and/or numeric expressions set equal to each other Face – a flat surface of a three-dimensional figure Height of a rectangul ...
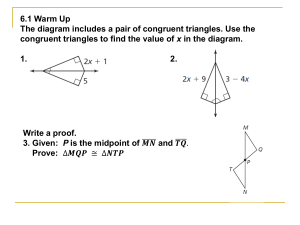
6.1 Warm Up The diagram includes a pair of congruent triangles
... This tool allows you to find the distance between two points or the length of a segment. This allows you to move the entire picture. Use these to zoom in or out as needed. ...
... This tool allows you to find the distance between two points or the length of a segment. This allows you to move the entire picture. Use these to zoom in or out as needed. ...
The Chicago High School for the Arts Honors Geometry Unit 3
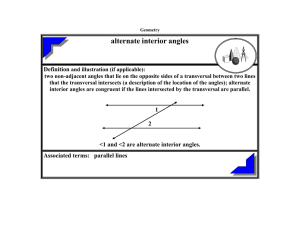
... 2) If two line segments are congruent, what things about them are the same? What things are different? ...
... 2) If two line segments are congruent, what things about them are the same? What things are different? ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)