Geometry Nomenclature: Triangles
... are larger. Children enjoy using a measuring angle to find different types of these angles in the environment. Children can then identify triangles that have these angles. One example of each should be recorded on paper. Activity 4 After they have learned the terminology they can name triangles such ...
... are larger. Children enjoy using a measuring angle to find different types of these angles in the environment. Children can then identify triangles that have these angles. One example of each should be recorded on paper. Activity 4 After they have learned the terminology they can name triangles such ...
239 Lesson 5 . 2
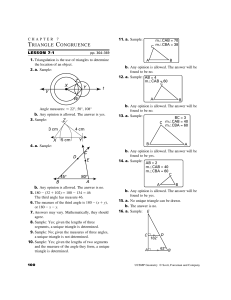
... using the Corresponding Angles Theorem. Since ∠ABC is congruent to ¯ is congruent to DF ¯, then one pair of corresponding angles ∠DEF and AC and two pairs of non-included corresponding sides are congruent. This means that △ABC is congruent to △DEF using the AAS Triangle Congruence Theorem. ...
... using the Corresponding Angles Theorem. Since ∠ABC is congruent to ¯ is congruent to DF ¯, then one pair of corresponding angles ∠DEF and AC and two pairs of non-included corresponding sides are congruent. This means that △ABC is congruent to △DEF using the AAS Triangle Congruence Theorem. ...
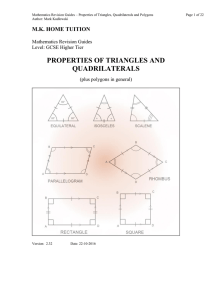
TRIANGLE CONGRUENCE
... 7. Key question: Can a given region tessellate the plane? 8. One museum where many tessellations can be found is the Alhambra. 9. Yes. Since the sum of the angle measures in ABCD is 360, it is possible to have a different angle from each of the four congruent quadrilaterals meeting at a single point ...
... 7. Key question: Can a given region tessellate the plane? 8. One museum where many tessellations can be found is the Alhambra. 9. Yes. Since the sum of the angle measures in ABCD is 360, it is possible to have a different angle from each of the four congruent quadrilaterals meeting at a single point ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)