2205 Unit 1 NOTES - North Penn School District
... Every point on a line can be paired with a real number, called the coordinate of the point. The distance between any two points on the number line is the ___________________ ___________________ of the ____________________ of the coordinates. ...
... Every point on a line can be paired with a real number, called the coordinate of the point. The distance between any two points on the number line is the ___________________ ___________________ of the ____________________ of the coordinates. ...
Geometry Name Manning Unit 3 Test Review: Part 1 Identify each
... Unit 3 Test Review: Part 1 Identify each statement as true or false. Justify your answer (true or false) by either using a conjecture or a clear explanation that can (but doesn’t have to) include a labeled diagram. 1) If one of the base angles of an isosceles triangle is 22°, then the vertex angle h ...
... Unit 3 Test Review: Part 1 Identify each statement as true or false. Justify your answer (true or false) by either using a conjecture or a clear explanation that can (but doesn’t have to) include a labeled diagram. 1) If one of the base angles of an isosceles triangle is 22°, then the vertex angle h ...
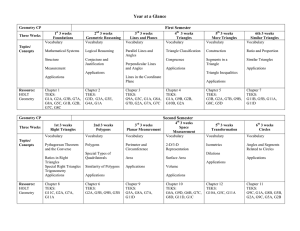
Year at a Glance First Semester
... TEKS The student will: -compute ratios and use proportions to solve problems. -solve percent and probability problems. -identify the conditions that ensure two polygons are similar. -use properties of similar polygons to solve problems. -recognize the conditions that ensure two triangles are similar ...
... TEKS The student will: -compute ratios and use proportions to solve problems. -solve percent and probability problems. -identify the conditions that ensure two polygons are similar. -use properties of similar polygons to solve problems. -recognize the conditions that ensure two triangles are similar ...
Daily Lesson Plan Format For Vertical Team - bcps-ap-math
... Notes: Power Point: “What is a polygon?” (closed-sided figure, 3 sides or more, straight sides), what is a quadrilateral? (4-sided polygon), name other polygons (triangle, hexagon, heptagon, etc), what does it mean for a polygon to be convex/concave? (convex – sides out, concave – some sides may “ca ...
... Notes: Power Point: “What is a polygon?” (closed-sided figure, 3 sides or more, straight sides), what is a quadrilateral? (4-sided polygon), name other polygons (triangle, hexagon, heptagon, etc), what does it mean for a polygon to be convex/concave? (convex – sides out, concave – some sides may “ca ...
File
... Advanced Geometry Section 3.8 The HL Postulate Learner Objective: Students will solve proofs and problems using the HL Postulate of triangle congruence. ...
... Advanced Geometry Section 3.8 The HL Postulate Learner Objective: Students will solve proofs and problems using the HL Postulate of triangle congruence. ...
Geometry Curriculum Map Table of Contents Unit 1
... Vocabulary: Geometric mean, Tangent, Sine, Cosine, Angle of Elevation, Angle of Depression ...
... Vocabulary: Geometric mean, Tangent, Sine, Cosine, Angle of Elevation, Angle of Depression ...
Understanding Congruence with Reflections, Rotations, and
... The base angles of an isosceles triangle are congruent. Vertical angles are congruent. A parallelogram has opposite sides and angles congruent. If a quadrilateral has diagonals that are perpendicular bisectors of each other, then it is a rhombus. If two lines are parallel, a transversal creates cong ...
... The base angles of an isosceles triangle are congruent. Vertical angles are congruent. A parallelogram has opposite sides and angles congruent. If a quadrilateral has diagonals that are perpendicular bisectors of each other, then it is a rhombus. If two lines are parallel, a transversal creates cong ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)