Math information – notes from class OPERATIONS: ADD
... RADIUS – the distance from the center to any point on the circle. DIAMETER – The distance across the circle through its center The diameter is twice the radius. CIRCUMFERENCE – The distance around the circle. ...
... RADIUS – the distance from the center to any point on the circle. DIAMETER – The distance across the circle through its center The diameter is twice the radius. CIRCUMFERENCE – The distance around the circle. ...
8 Math standards Quarter 2
... the equations. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6. c. Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of ...
... the equations. Solve simple cases by inspection. For example, 3x + 2y = 5 and 3x + 2y = 6 have no solution because 3x + 2y cannot simultaneously be 5 and 6. c. Solve real-world and mathematical problems leading to two linear equations in two variables. For example, given coordinates for two pairs of ...
Applications of Vectors
... Two draft horses are pulling on a tree stump with forces of 250 pounds and 280 pounds as shown. If the angle between the forces is 60°, then what is the magnitude of the resultant force? What is the angle between the resultant and the 280 pound force? ...
... Two draft horses are pulling on a tree stump with forces of 250 pounds and 280 pounds as shown. If the angle between the forces is 60°, then what is the magnitude of the resultant force? What is the angle between the resultant and the 280 pound force? ...
Revised Version 070516
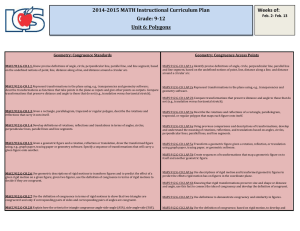
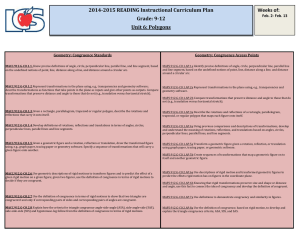
... By definition, two polygons are similar if and only if their corresponding angles are congruent and their corresponding side lengths are proportional. Thus, similar figures may have different sizes, but they have the same shape. The following foci incorporate a variety of approaches (geometric, grap ...
... By definition, two polygons are similar if and only if their corresponding angles are congruent and their corresponding side lengths are proportional. Thus, similar figures may have different sizes, but they have the same shape. The following foci incorporate a variety of approaches (geometric, grap ...
unit evaluation rubric
... Essential Outcomes: (must be assessed for mastery) Problem solving and higher order thinking components are essential for ‘A’ level mastery. Each outcome can contain problem solving and higher order thinking components (as found in suggested text). 1. The Student Will identify and solve parallel, pe ...
... Essential Outcomes: (must be assessed for mastery) Problem solving and higher order thinking components are essential for ‘A’ level mastery. Each outcome can contain problem solving and higher order thinking components (as found in suggested text). 1. The Student Will identify and solve parallel, pe ...
Cumulative Test 8
... acute, then the triangle is an acute triangle. B If two angles of a triangle are congruent, then the sides opposite them are congruent. C If the sum of two angles of a triangle is more than 90°, then one of the two angles is obtuse. D If no two angles of a triangle are congruent, then the triangle i ...
... acute, then the triangle is an acute triangle. B If two angles of a triangle are congruent, then the sides opposite them are congruent. C If the sum of two angles of a triangle is more than 90°, then one of the two angles is obtuse. D If no two angles of a triangle are congruent, then the triangle i ...
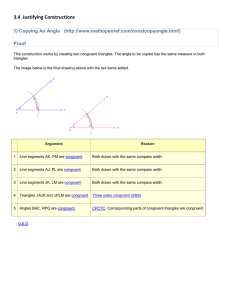
Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.For more than two thousand years, the adjective ""Euclidean"" was unnecessary because no other sort of geometry had been conceived. Euclid's axioms seemed so intuitively obvious (with the possible exception of the parallel postulate) that any theorem proved from them was deemed true in an absolute, often metaphysical, sense. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. An implication of Albert Einstein's theory of general relativity is that physical space itself is not Euclidean, and Euclidean space is a good approximation for it only where the gravitational field is weak.Euclidean geometry is an example of synthetic geometry, in that it proceeds logically from axioms to propositions without the use of coordinates. This is in contrast to analytic geometry, which uses coordinates.