Ratio Based on Right Triangles
... In each of the following pairs of figures, the red one is obtained by transforming the blue one about the fixed point x. Determine (i) which type of transformation (translation, rotation, reflection, enlargement, reduction) it is, (ii) whether the two figures are congruent or not. ...
... In each of the following pairs of figures, the red one is obtained by transforming the blue one about the fixed point x. Determine (i) which type of transformation (translation, rotation, reflection, enlargement, reduction) it is, (ii) whether the two figures are congruent or not. ...
Geometry Module 1, Topic B, Lesson 6: Teacher Version
... vocabulary is critical and students should be able to define the relevant terms themselves. It may be useful to draw or discuss counterexamples of a few terms and ask students to explain why they do not fit a particular definition. As students work on problems, encourage them to show each step of th ...
... vocabulary is critical and students should be able to define the relevant terms themselves. It may be useful to draw or discuss counterexamples of a few terms and ask students to explain why they do not fit a particular definition. As students work on problems, encourage them to show each step of th ...
Triangles
... of the lengths of any two sides of a triangle is greater than the length of the third side. We will determine the sum of the interior angles for any triangle. ...
... of the lengths of any two sides of a triangle is greater than the length of the third side. We will determine the sum of the interior angles for any triangle. ...
Export - CPalms
... A city constructed a triangular park bounded by three paved walking paths. The paths are 70, 100 and 130 yards in length, respectively. The planning committee is seeking a consultant's advice on where to locate structures within the park. They can't agree on a location for either a large fountain or ...
... A city constructed a triangular park bounded by three paved walking paths. The paths are 70, 100 and 130 yards in length, respectively. The planning committee is seeking a consultant's advice on where to locate structures within the park. They can't agree on a location for either a large fountain or ...
Angles and Parallel Lines
... each pair of consecutive interior angles is supplementary (sum to 180o). You will prove this theorem as a homework problem! ...
... each pair of consecutive interior angles is supplementary (sum to 180o). You will prove this theorem as a homework problem! ...
Geometry Accelerated! - Clifton Public Schools
... A ray begins at a point and extends infinitely in one direction. You need two letters to name a ray. The first letter is the endpoint of the ray, and the second letter is any other point that the ray passes through. ...
... A ray begins at a point and extends infinitely in one direction. You need two letters to name a ray. The first letter is the endpoint of the ray, and the second letter is any other point that the ray passes through. ...
x - Greater Nanticoke Area School District
... CS 2.5.11A: Solve non-routine and multi-step problems 57. Apply basic rules of real numbers in problem solving 58. Select and justify appropriate methods needed in solving multi-step problems CS 2.5.11B: Use representations to communicate mathematically 59. Translate words to symbols and symbols to ...
... CS 2.5.11A: Solve non-routine and multi-step problems 57. Apply basic rules of real numbers in problem solving 58. Select and justify appropriate methods needed in solving multi-step problems CS 2.5.11B: Use representations to communicate mathematically 59. Translate words to symbols and symbols to ...
Euclidean geometry

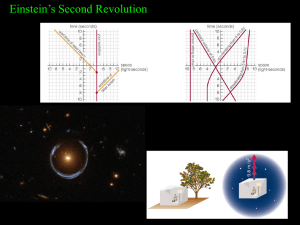
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.For more than two thousand years, the adjective ""Euclidean"" was unnecessary because no other sort of geometry had been conceived. Euclid's axioms seemed so intuitively obvious (with the possible exception of the parallel postulate) that any theorem proved from them was deemed true in an absolute, often metaphysical, sense. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. An implication of Albert Einstein's theory of general relativity is that physical space itself is not Euclidean, and Euclidean space is a good approximation for it only where the gravitational field is weak.Euclidean geometry is an example of synthetic geometry, in that it proceeds logically from axioms to propositions without the use of coordinates. This is in contrast to analytic geometry, which uses coordinates.