A Picture is Worth a Thousand Words
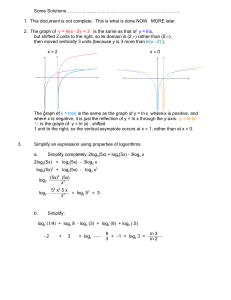
... of values and by plotting the x and y−intercepts. In addition, you will learn about the domain and the range of functions, what these terms mean, what proper notation is, and how to determine these from a graph. The chapter will continue with graphing a quadratic function of the form y = x2 . In thi ...
... of values and by plotting the x and y−intercepts. In addition, you will learn about the domain and the range of functions, what these terms mean, what proper notation is, and how to determine these from a graph. The chapter will continue with graphing a quadratic function of the form y = x2 . In thi ...
Fast Nearest Neighbor Search on Large Time
... We work with large graphs (that do not fit in main memory), thus cluster vertices such that each cluster is “small enough”. Need “good” clusters—many intra-cluster edges, but few inter-cluster edges. q q ...
... We work with large graphs (that do not fit in main memory), thus cluster vertices such that each cluster is “small enough”. Need “good” clusters—many intra-cluster edges, but few inter-cluster edges. q q ...
Graphs - Images
... would be from 2 – 22 and you want the scale to fit the graph. • The best interval would be to go by 5’s. ...
... would be from 2 – 22 and you want the scale to fit the graph. • The best interval would be to go by 5’s. ...
Set 2
... For each (distinct) pair of points in the set, compute a, b, and c to define the line ax + by = c. For each other point, plug its x and y coordinates into the expression ax + by – c. If, for all the other points (x,y), ax + by – c has the same sign (all positive or all negative), then this pair ...
... For each (distinct) pair of points in the set, compute a, b, and c to define the line ax + by = c. For each other point, plug its x and y coordinates into the expression ax + by – c. If, for all the other points (x,y), ax + by – c has the same sign (all positive or all negative), then this pair ...
statistical graphs complexity and reading levels: a study with
... either expression or content in a semiotic function. According to these authors, the semiotic functions, and hence the meaning, can be personal or institutional, unitary or systemic (Godino et al., 2007). In agreement with Peirce’s semiotics (1978 /1965), the onto-semiotic approach assumes that both ...
... either expression or content in a semiotic function. According to these authors, the semiotic functions, and hence the meaning, can be personal or institutional, unitary or systemic (Godino et al., 2007). In agreement with Peirce’s semiotics (1978 /1965), the onto-semiotic approach assumes that both ...
Version 2
... SET: Given a positive integer p and a graph G, does G have an irreversible k-conversion set of size at most p? Theorem (Dreyer 2000): IRREVERSIBLE kCONVERSION SET is NP-complete for fixed k > ...
... SET: Given a positive integer p and a graph G, does G have an irreversible k-conversion set of size at most p? Theorem (Dreyer 2000): IRREVERSIBLE kCONVERSION SET is NP-complete for fixed k > ...
Acyclic Type of Relationships Between Autonomous
... for the AToR and the k-AToR problems. In these analyses we consider solutions that contain only directed edges (i.e. edges of type customer-provider). One can argue that this requirement is stricter than necessary and therefore does not reflect the real practical problem. Yet, as we prove in the nex ...
... for the AToR and the k-AToR problems. In these analyses we consider solutions that contain only directed edges (i.e. edges of type customer-provider). One can argue that this requirement is stricter than necessary and therefore does not reflect the real practical problem. Yet, as we prove in the nex ...
etri03-part1 - Princeton University
... – Extracted set of unique paths P for each view – Applied reverse pruning algorithm to each view – Applied inference rules to the vectors of ranks ...
... – Extracted set of unique paths P for each view – Applied reverse pruning algorithm to each view – Applied inference rules to the vectors of ranks ...
Graphing Exponential Functions
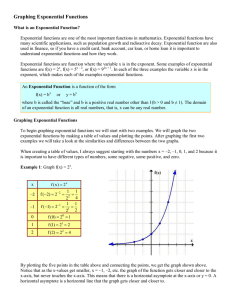
... Graphing an Exponential Function with a Vertical Shift An exponential function of the form f(x) = b x + k is an exponential function with a vertical shift. The constant k is what causes the vertical shift to occur.A vertical shift is when the graph of the function is moved up or down a fixed di ...
... Graphing an Exponential Function with a Vertical Shift An exponential function of the form f(x) = b x + k is an exponential function with a vertical shift. The constant k is what causes the vertical shift to occur.A vertical shift is when the graph of the function is moved up or down a fixed di ...
Improving Planning Graph Analysis for Artificial Intelligence Planning
... by an action, and (b) no action may be removed from the set without making (a) no longer true. Figure 4 shows an example of a non-minimal set of actions. When a non-minimal set of actions is found, the search procedure is immediately backtracked and another combination is tried. When the planning do ...
... by an action, and (b) no action may be removed from the set without making (a) no longer true. Figure 4 shows an example of a non-minimal set of actions. When a non-minimal set of actions is found, the search procedure is immediately backtracked and another combination is tried. When the planning do ...
Solving Equations using Inverse Operations
... he buy and stay within the limit? a) Write an inequality to model the problem. b) Solve the inequality and interpret the solution. ...
... he buy and stay within the limit? a) Write an inequality to model the problem. b) Solve the inequality and interpret the solution. ...
Drawing Clustered Graphs - School of Information Technologies
... Academic delegate: “Well, planarity is a central concept even for non-planar graphs. To be able to draw general graphs, we find a topology with a small number of edge crossings, model this topology as a planar graph, and draw that planar graph.” Industry delegate: “Sounds good. But I don’t know how ...
... Academic delegate: “Well, planarity is a central concept even for non-planar graphs. To be able to draw general graphs, we find a topology with a small number of edge crossings, model this topology as a planar graph, and draw that planar graph.” Industry delegate: “Sounds good. But I don’t know how ...
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called ""colors"" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges share the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.Vertex coloring is the starting point of the subject, and other coloring problems can be transformed into a vertex version. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex coloring of its dual. However, non-vertex coloring problems are often stated and studied as is. That is partly for perspective, and partly because some problems are best studied in non-vertex form, as for instance is edge coloring.The convention of using colors originates from coloring the countries of a map, where each face is literally colored. This was generalized to coloring the faces of a graph embedded in the plane. By planar duality it became coloring the vertices, and in this form it generalizes to all graphs. In mathematical and computer representations, it is typical to use the first few positive or nonnegative integers as the ""colors"". In general, one can use any finite set as the ""color set"". The nature of the coloring problem depends on the number of colors but not on what they are.Graph coloring enjoys many practical applications as well as theoretical challenges. Beside the classical types of problems, different limitations can also be set on the graph, or on the way a color is assigned, or even on the color itself. It has even reached popularity with the general public in the form of the popular number puzzle Sudoku. Graph coloring is still a very active field of research.Note: Many terms used in this article are defined in Glossary of graph theory.









![[CP11] The Next-to-Shortest Path Problem on](http://s1.studyres.com/store/data/019681272_1-7e1f7e9170c466fbb6bdb289dfe09b5d-300x300.png)