A Heuristic for a Mixed Integer Program using the Characteristic
... global optimal solution. The major disadvantages of existing methods like round off errors, and creation or emergence of many sub-problems (branches), is the time taken to obtain the optimal solution and failure to obtain global optimal solutions. These justify the need to find better approaches for ...
... global optimal solution. The major disadvantages of existing methods like round off errors, and creation or emergence of many sub-problems (branches), is the time taken to obtain the optimal solution and failure to obtain global optimal solutions. These justify the need to find better approaches for ...
Preliminary review / Publisher`s description: This self
... finite-dimensional optimization problems, and the Pontryagin principle, for dynamic optimization problems. The particular versions of the Fermat-Lagrange principle for the different classes of mathematical programming problems considered in this book (all of them involving differentiable and/or conv ...
... finite-dimensional optimization problems, and the Pontryagin principle, for dynamic optimization problems. The particular versions of the Fermat-Lagrange principle for the different classes of mathematical programming problems considered in this book (all of them involving differentiable and/or conv ...
Binary Integer Programming in associative data models
... number of state variables (i.e. the size of x) and m is the number of constraints. Similarly, A is an m × n matrix. Elements of c, b and A are real numbers. An LP without solutions on the domain is called infeasible, while a particular assignment of variables e x satisfying the constraints Ax ≤ b is ...
... number of state variables (i.e. the size of x) and m is the number of constraints. Similarly, A is an m × n matrix. Elements of c, b and A are real numbers. An LP without solutions on the domain is called infeasible, while a particular assignment of variables e x satisfying the constraints Ax ≤ b is ...
TCSS 343: Large Integer Multiplication Suppose we want to multiply
... Let T(n) be the time it takes to multiply two n-bit integers using the algorithm above. Then the following recurrence equation applies: T(1) = 1 T(n) = 3 T(n/2) + cn Since we can multiply two 1-bit integers in constant time, T(1) = 1. (If we wanted to be more accurate, we would say T(1) = d, for som ...
... Let T(n) be the time it takes to multiply two n-bit integers using the algorithm above. Then the following recurrence equation applies: T(1) = 1 T(n) = 3 T(n/2) + cn Since we can multiply two 1-bit integers in constant time, T(1) = 1. (If we wanted to be more accurate, we would say T(1) = d, for som ...
Achieving Maximum Energy-Efficiency in Multi-Relay
... frequency division multiple access (OFDMA) cellular network, where the objective function is formulated as the ratio of the spectral-efficiency (SE) over the total power dissipation. It is proven that the fractional programming problem considered is quasi-concave so that Dinkelbach’s method may be e ...
... frequency division multiple access (OFDMA) cellular network, where the objective function is formulated as the ratio of the spectral-efficiency (SE) over the total power dissipation. It is proven that the fractional programming problem considered is quasi-concave so that Dinkelbach’s method may be e ...
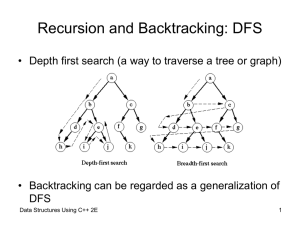
Recursion
... The process of solving a problem by reducing it to smaller versions of itself is called recursion. Example: Consider the concept of factorials ...
... The process of solving a problem by reducing it to smaller versions of itself is called recursion. Example: Consider the concept of factorials ...
Quadratic optimization over a second-order cone with linear equality
... cone constrained quadratic optimization problem [7, 18]. Some studies of optimization problems over L can be found in [1–3, 6]. Recently, linear conic programming has received much attention for solving quadratic optimization problems [5]. Sturm and Zhang introduced cones of nonnegative quadratic fu ...
... cone constrained quadratic optimization problem [7, 18]. Some studies of optimization problems over L can be found in [1–3, 6]. Recently, linear conic programming has received much attention for solving quadratic optimization problems [5]. Sturm and Zhang introduced cones of nonnegative quadratic fu ...
Recursion
... Recursion • While recursion can be used to solve many problems it is not always the most efficient solution int factorial (int n) { int fact = 1; for (int k = 1; k <= n; k++) fact = fact * k; return fact; } // factorial ...
... Recursion • While recursion can be used to solve many problems it is not always the most efficient solution int factorial (int n) { int fact = 1; for (int k = 1; k <= n; k++) fact = fact * k; return fact; } // factorial ...
A Simulation Approach to Optimal Stopping Under Partial Information
... frameworks. When the transition density of the state variables is known, classical (a) dynamic programming computations are possible, see e.g. [38]. If the problem state is low-dimensional and Markov, one may alternatively use the quasi-variational formulation to obtain a free-boundary partial diffe ...
... frameworks. When the transition density of the state variables is known, classical (a) dynamic programming computations are possible, see e.g. [38]. If the problem state is low-dimensional and Markov, one may alternatively use the quasi-variational formulation to obtain a free-boundary partial diffe ...
degrees radians 36 radians radians radians π ⋅ = 180° π ° ⋅ = 180
... Use the fact that both coordinates of the point on the terminal side are positive to find that the quadrant the terminal side lies in. E. Incorrect! Use the fact that both coordinates of the point on the terminal side are positive to find that the quadrant the terminal side lies in. The points in qu ...
... Use the fact that both coordinates of the point on the terminal side are positive to find that the quadrant the terminal side lies in. E. Incorrect! Use the fact that both coordinates of the point on the terminal side are positive to find that the quadrant the terminal side lies in. The points in qu ...
Problem of the Week - Sino Canada School
... count the number of emails but leave all of the emails unread. At the end of the first day there were 2 unread emails. At the end of the second day there were 5 unread emails, an increase of 3 emails from the previous day. At the end of the third day there were 12 unread emails, an increase of 7 ema ...
... count the number of emails but leave all of the emails unread. At the end of the first day there were 2 unread emails. At the end of the second day there were 5 unread emails, an increase of 3 emails from the previous day. At the end of the third day there were 12 unread emails, an increase of 7 ema ...
The theory of optimal stopping
... inference, and the third in the statistical design of experiments. The chapter concludes with a formulation of the general optimal stopping problem on random sequences. ...
... inference, and the third in the statistical design of experiments. The chapter concludes with a formulation of the general optimal stopping problem on random sequences. ...
Optimal Policies for a Class of Restless Multiarmed
... in helping to identify and verify optimal policies for similar multiarmed bandit problems and for developing good suboptimal solutions for more complex problems. The latter is illustrated by the work in [3] and [13]. In both cases, a priority index rule is proven to be optimal for special cases of a ...
... in helping to identify and verify optimal policies for similar multiarmed bandit problems and for developing good suboptimal solutions for more complex problems. The latter is illustrated by the work in [3] and [13]. In both cases, a priority index rule is proven to be optimal for special cases of a ...
slides
... Other solutions To construct an iMZ , we have to check four constraints : i. Muu = (1 − Zu ) ii. 0 ≤ M u iii. M u ≤ 1 − Z iv. M u ≤ M v for u < v These constraints are easy to handle if M u are solutions of a SDE: The constraint i indicates the initial condition; the constraint ii means that we must ...
... Other solutions To construct an iMZ , we have to check four constraints : i. Muu = (1 − Zu ) ii. 0 ≤ M u iii. M u ≤ 1 − Z iv. M u ≤ M v for u < v These constraints are easy to handle if M u are solutions of a SDE: The constraint i indicates the initial condition; the constraint ii means that we must ...
Routing
... ◦ Claim 2. Dj is, for each j, the shortest distance between j and 1, using paths whose nodes all belong to P (except, possibly, j) • Given the above two properties ◦ When algorithm stops, the shortest path lengths must be equal to Dj , for all j → That is, algorithm finds the shortest path as desire ...
... ◦ Claim 2. Dj is, for each j, the shortest distance between j and 1, using paths whose nodes all belong to P (except, possibly, j) • Given the above two properties ◦ When algorithm stops, the shortest path lengths must be equal to Dj , for all j → That is, algorithm finds the shortest path as desire ...
Recursion Review - Department of Computer Science
... int last_but_one; // second previous Fibonacci number, Fi−2 int last_value; // previous Fibonacci number, Fi−1 int current; // current Fibonacci number Fi if (n <= 0) return 0; else if (n == 1) return 1; else { ...
... int last_but_one; // second previous Fibonacci number, Fi−2 int last_value; // previous Fibonacci number, Fi−1 int current; // current Fibonacci number Fi if (n <= 0) return 0; else if (n == 1) return 1; else { ...
Scalability_1.1
... → If W < Θ(p) i.e problem size grows slower than p, as p↑ ↑ => at one point #PE > W =>E↓ ↓ => asymptotically W= Θ(p) Problem size must increase proportional as Θ(p) to maintain fixed efficiency W = Ω(p) (W should grow at least as fast as p) Ω(p) is the asymptotic lower bound on the isoefficiency fun ...
... → If W < Θ(p) i.e problem size grows slower than p, as p↑ ↑ => at one point #PE > W =>E↓ ↓ => asymptotically W= Θ(p) Problem size must increase proportional as Θ(p) to maintain fixed efficiency W = Ω(p) (W should grow at least as fast as p) Ω(p) is the asymptotic lower bound on the isoefficiency fun ...
Full text
... G.E. Andrews proposed the following problem. Show that Fp+i(q) is divisible by 7 +q+~- + qp~7, where p is any prime = ±2 (mod 51 For proof see [3]. This result is by no means apparent from (3.2). The proof depends upon the identity Fn+1 - £(-Vkx'/*k(5k-V[e'!k)] ...
... G.E. Andrews proposed the following problem. Show that Fp+i(q) is divisible by 7 +q+~- + qp~7, where p is any prime = ±2 (mod 51 For proof see [3]. This result is by no means apparent from (3.2). The proof depends upon the identity Fn+1 - £(-Vkx'/*k(5k-V[e'!k)] ...
Optimal consumption and portfolio choice with borrowing constraints
... problem a nonlinear partial differential equation, namely the Bellman equation. We show that if the utility function satisfies some general regularity conditions, the Bellman equation has a unique solution which is twice continuously differentiable. Using a verification theorem, this solution turns ...
... problem a nonlinear partial differential equation, namely the Bellman equation. We show that if the utility function satisfies some general regularity conditions, the Bellman equation has a unique solution which is twice continuously differentiable. Using a verification theorem, this solution turns ...
A Nonlinear Programming Algorithm for Solving Semidefinite
... is easily seen to be equivalent to (1) since every X 0 can be factored as V V T for some V . Since the positive semidefiniteness constraint has been eliminated, (2) has a significant advantage over (1), but this benefit has a corresponding cost: the objective function and constraints are no longer ...
... is easily seen to be equivalent to (1) since every X 0 can be factored as V V T for some V . Since the positive semidefiniteness constraint has been eliminated, (2) has a significant advantage over (1), but this benefit has a corresponding cost: the objective function and constraints are no longer ...
Idan Maor
... for a fixed vector r we only need to compute the K min cost max flow problems. • The objective function of the resource allocation problem z(r) is piecewise linear convex function of r. • Both properties(the convexity and the piecewise linearity), derived from the fact that the resource allocation i ...
... for a fixed vector r we only need to compute the K min cost max flow problems. • The objective function of the resource allocation problem z(r) is piecewise linear convex function of r. • Both properties(the convexity and the piecewise linearity), derived from the fact that the resource allocation i ...
Optimization Techniques
... The values inside the node show the value of state variable at each stage ...
... The values inside the node show the value of state variable at each stage ...
Example 1. Insufficiency of the optimality conditions
... We have described the general scheme for solving optimal control problems and considered a specific example that proved our scheme to be highly effective. However, perfect situations like this are by no means frequent. Unfortunately, there are numerous obstacles on the way of solving optimization pr ...
... We have described the general scheme for solving optimal control problems and considered a specific example that proved our scheme to be highly effective. However, perfect situations like this are by no means frequent. Unfortunately, there are numerous obstacles on the way of solving optimization pr ...
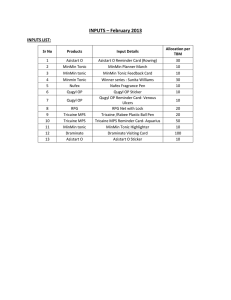
INPUTS – February 2013
... combination with Ornidazole is beneficial as it is effective against anaerobes, when applied topically. Sir, introducing Qugyl-OP ointment, combination of povidone-iodine and ornidazole, that outclasses plain povidone-iodine. Qugyl-OP ointment, offers complete treatment and is available at Rs. 49/Tu ...
... combination with Ornidazole is beneficial as it is effective against anaerobes, when applied topically. Sir, introducing Qugyl-OP ointment, combination of povidone-iodine and ornidazole, that outclasses plain povidone-iodine. Qugyl-OP ointment, offers complete treatment and is available at Rs. 49/Tu ...
Dynamic programming
In mathematics, computer science, economics, and bioinformatics, dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems and optimal substructure (described below). When applicable, the method takes far less time than other methods that don't take advantage of the subproblem overlap (like depth-first search).In order to solve a given problem using a dynamic programming approach, we need to solve different parts of the problem (subproblems), then combine the solutions of the subproblems to reach an overall solution. Often when using a more naive method, many of the subproblems are generated and solved many times. The dynamic programming approach seeks to solve each subproblem only once, thus reducing the number of computations: once the solution to a given subproblem has been computed, it is stored or ""memoized"": the next time the same solution is needed, it is simply looked up. This approach is especially useful when the number of repeating subproblems grows exponentially as a function of the size of the input.Dynamic programming algorithms are used for optimization (for example, finding the shortest path between two points, or the fastest way to multiply many matrices). A dynamic programming algorithm will examine the previously solved subproblems and will combine their solutions to give the best solution for the given problem. The alternatives are many, such as using a greedy algorithm, which picks the locally optimal choice at each branch in the road. The locally optimal choice may be a poor choice for the overall solution. While a greedy algorithm does not guarantee an optimal solution, it is often faster to calculate. Fortunately, some greedy algorithms (such as minimum spanning trees) are proven to lead to the optimal solution.For example, let's say that you have to get from point A to point B as fast as possible, in a given city, during rush hour. A dynamic programming algorithm will look at finding the shortest paths to points close to A, and use those solutions to eventually find the shortest path to B. On the other hand, a greedy algorithm will start you driving immediately and will pick the road that looks the fastest at every intersection. As you can imagine, this strategy might not lead to the fastest arrival time, since you might take some ""easy"" streets and then find yourself hopelessly stuck in a traffic jam.Sometimes, applying memoization to a naive basic recursive solution already results in a dynamic programming solution with asymptotically optimal time complexity; however, the optimal solution to some problems requires more sophisticated dynamic programming algorithms. Some of these may be recursive as well but parametrized differently from the naive solution. Others can be more complicated and cannot be implemented as a recursive function with memoization. Examples of these are the two solutions to the Egg Dropping puzzle below.