![[edit] Construction of the Lebesgue measure](http://s1.studyres.com/store/data/001141507_1-534aa5aeea25b32a8226835f0ebc16e0-300x300.png)
TROPICAL GEOMETRY, LECTURE 4 1. MS §3.1 TRoPiCAl
... contained in the LHS. For the opposite, note that if f ∈ I, then f d ∈ I for some d ≥ 1, and by the consequence to Kapranov’s theorem, trop(V (f d )) = trop(V (f )). • Lemma: When I = (f ), the definition above agrees with our definition earlier. Indeed, for each g ∈ (f ), say g = hf , we have trop( ...
... contained in the LHS. For the opposite, note that if f ∈ I, then f d ∈ I for some d ≥ 1, and by the consequence to Kapranov’s theorem, trop(V (f d )) = trop(V (f )). • Lemma: When I = (f ), the definition above agrees with our definition earlier. Indeed, for each g ∈ (f ), say g = hf , we have trop( ...
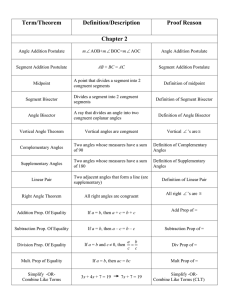
Axioms of Incidence Geometry Incidence Axiom 1. There exist at
... Lemma 3.3 (Ruler Sliding Lemma). Suppose ` is a line and f W ` ! R is a coordinate function for `. Given a real number c, define a new function f1 W ` ! R by f1 .X/ D f .X/ C c for all X 2 `. Then f1 is also a coordinate function for `. Lemma 3.4 (Ruler Flipping Lemma). Suppose ` is a line and f W ` ...
... Lemma 3.3 (Ruler Sliding Lemma). Suppose ` is a line and f W ` ! R is a coordinate function for `. Given a real number c, define a new function f1 W ` ! R by f1 .X/ D f .X/ C c for all X 2 `. Then f1 is also a coordinate function for `. Lemma 3.4 (Ruler Flipping Lemma). Suppose ` is a line and f W ` ...
Riemann–Roch theorem
The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles. It relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus g, in a way that can be carried over into purely algebraic settings.Initially proved as Riemann's inequality by Riemann (1857), the theorem reached its definitive form for Riemann surfaces after work of Riemann's short-lived student Gustav Roch (1865). It was later generalized to algebraic curves, to higher-dimensional varieties and beyond.