Functions
... The student will become familiar with relations, or sets of ordered pairs. He or she will learn how to tell if a relation is a function. This can be done by examining the sets of ordered pairs to see if each x-value corresponds to only one y-value. Graphically, you can see if a relation is a functio ...
... The student will become familiar with relations, or sets of ordered pairs. He or she will learn how to tell if a relation is a function. This can be done by examining the sets of ordered pairs to see if each x-value corresponds to only one y-value. Graphically, you can see if a relation is a functio ...
Mathematical Logic Deciding logical consequence Complexity of
... If B is derived by MP form Ai and Aj = Ai ⊃ B. Then, Ai and Aj = Ai ⊃ B, are provable in less then n steps and, by induction hypothesis, Γ ` A ⊃ Ai and Γ ` A ⊃ (Ai ⊃ B). Starting from the deductions of these two formulas from Γ, we can build a deduction of A ⊃ B form Γ as follows: ...
... If B is derived by MP form Ai and Aj = Ai ⊃ B. Then, Ai and Aj = Ai ⊃ B, are provable in less then n steps and, by induction hypothesis, Γ ` A ⊃ Ai and Γ ` A ⊃ (Ai ⊃ B). Starting from the deductions of these two formulas from Γ, we can build a deduction of A ⊃ B form Γ as follows: ...
Mathematics for Computer Science/Software Engineering
... something like this, all we need to do is to consider all those values of x for which P (x) is actually true, and show that in these cases Q(x) is also true. Such a proof is called a direct proof. But just as p → q is logically equivalent to q → p, we can see that ∀x(P (x) → Q(x)) is logically equiv ...
... something like this, all we need to do is to consider all those values of x for which P (x) is actually true, and show that in these cases Q(x) is also true. Such a proof is called a direct proof. But just as p → q is logically equivalent to q → p, we can see that ∀x(P (x) → Q(x)) is logically equiv ...
Propositional and predicate logic - Computing Science
... program syntax is correct and program execution does not result in division by zero. Argument 2: ...
... program syntax is correct and program execution does not result in division by zero. Argument 2: ...
A Brief Note on Proofs in Pure Mathematics
... You should note that induction can only be applied when the statements are indexed by the natural numbers. There has to be a first case (the base case), and you have to have be able to move to the ‘next’ statement (the induction step). If the statements are indexed by real numbers, then there is no ...
... You should note that induction can only be applied when the statements are indexed by the natural numbers. There has to be a first case (the base case), and you have to have be able to move to the ‘next’ statement (the induction step). If the statements are indexed by real numbers, then there is no ...
Rational and Irrational Numbers
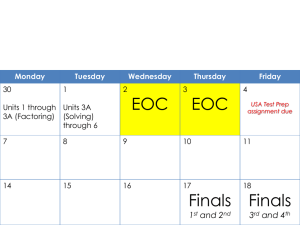
... • Ex: Joe started with $13. He has been saving $2 each week to purchase a baseball glove. Write a function that represents the amount of money in Joe’s bank account. • Ex: Rachel eats three cookies on the first day of the month. Each day she eats two more. Write a sequence for how many cookies she e ...
... • Ex: Joe started with $13. He has been saving $2 each week to purchase a baseball glove. Write a function that represents the amount of money in Joe’s bank account. • Ex: Rachel eats three cookies on the first day of the month. Each day she eats two more. Write a sequence for how many cookies she e ...
Introduction to Logic What is Logic? Simple Statements Which one is
... exclusively upon the truth values of its variables. The truth value of a proposition is known once the truth values of its variables are known. (See E.g. 30 - 32) ...
... exclusively upon the truth values of its variables. The truth value of a proposition is known once the truth values of its variables are known. (See E.g. 30 - 32) ...
axioms
... consistency because we produced a real world model for the system (i.e. actually two, the committee model and the graph model). • Note: It is true that we also produced a “non-model” (the books-shelves model) but this does not imply the system is not consistent. ...
... consistency because we produced a real world model for the system (i.e. actually two, the committee model and the graph model). • Note: It is true that we also produced a “non-model” (the books-shelves model) but this does not imply the system is not consistent. ...
Constructive Mathematics, in Theory and Programming Practice
... The notion defined by dropping from this definition the last clause, about preservation of equality, is called an operation. In the first part of this paper we shall have little to say about operations, but they will have more significance in the second part, when we discuss Martin-Löf’s theory of ...
... The notion defined by dropping from this definition the last clause, about preservation of equality, is called an operation. In the first part of this paper we shall have little to say about operations, but they will have more significance in the second part, when we discuss Martin-Löf’s theory of ...
Principia Mathematica

The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913. In 1927, it appeared in a second edition with an important Introduction To the Second Edition, an Appendix A that replaced ✸9 and an all-new Appendix C.PM, as it is often abbreviated, was an attempt to describe a set of axioms and inference rules in symbolic logic from which all mathematical truths could in principle be proven. As such, this ambitious project is of great importance in the history of mathematics and philosophy, being one of the foremost products of the belief that such an undertaking may be achievable. However, in 1931, Gödel's incompleteness theorem proved definitively that PM, and in fact any other attempt, could never achieve this lofty goal; that is, for any set of axioms and inference rules proposed to encapsulate mathematics, either the system must be inconsistent, or there must in fact be some truths of mathematics which could not be deduced from them.One of the main inspirations and motivations for PM was the earlier work of Gottlob Frege on logic, which Russell discovered allowed for the construction of paradoxical sets. PM sought to avoid this problem by ruling out the unrestricted creation of arbitrary sets. This was achieved by replacing the notion of a general set with the notion of a hierarchy of sets of different 'types', a set of a certain type only allowed to contain sets of strictly lower types. Contemporary mathematics, however, avoids paradoxes such as Russell's in less unwieldy ways, such as the system of Zermelo–Fraenkel set theory.PM is not to be confused with Russell's 1903 Principles of Mathematics. PM states: ""The present work was originally intended by us to be comprised in a second volume of Principles of Mathematics... But as we advanced, it became increasingly evident that the subject is a very much larger one than we had supposed; moreover on many fundamental questions which had been left obscure and doubtful in the former work, we have now arrived at what we believe to be satisfactory solutions.""The Modern Library placed it 23rd in a list of the top 100 English-language nonfiction books of the twentieth century.