File - MYP-3
... expressed as a decimal number between 1 and 10 multiplied by a power of 10 e( g, 7000 = 7 x 103 or 0.0000019 = 1.9 x 10 -6) ...
... expressed as a decimal number between 1 and 10 multiplied by a power of 10 e( g, 7000 = 7 x 103 or 0.0000019 = 1.9 x 10 -6) ...
File
... pronouns for nouns in English grammar or multiple name substitution. Unfortunately, in most of the Mathematical writings (books or articles) the difference is not given explicity, the reader has to distinguish the name and object according to the context. This kind of catastrophic events occurs whil ...
... pronouns for nouns in English grammar or multiple name substitution. Unfortunately, in most of the Mathematical writings (books or articles) the difference is not given explicity, the reader has to distinguish the name and object according to the context. This kind of catastrophic events occurs whil ...
Quantified Equilibrium Logic and the First Order Logic of Here
... answer set semantics, the underlying logic is the least strong negation extension of HT, denoted by N5 . As equilibrium logic is defined for arbitrary propositional formulas it yields an extension of the usual syntax of (ground) answer set programs. It also provides a useful logical foundation for an ...
... answer set semantics, the underlying logic is the least strong negation extension of HT, denoted by N5 . As equilibrium logic is defined for arbitrary propositional formulas it yields an extension of the usual syntax of (ground) answer set programs. It also provides a useful logical foundation for an ...
mgb6e_ppt_02_09 (1)
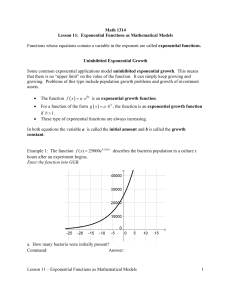
... 1. If a, b, and c are real numbers, and c is positive, then a < b and ac < bc are equivalent inequalities. 2. If a, b, and c are real numbers, and c is negative, then a < b and ac > bc are equivalent inequalities. ...
... 1. If a, b, and c are real numbers, and c is positive, then a < b and ac < bc are equivalent inequalities. 2. If a, b, and c are real numbers, and c is negative, then a < b and ac > bc are equivalent inequalities. ...
Basic Concepts needed for Chemistry
... express very large numbers. This method is called scientific notation. Scientific Notation is based on powers of the base number 10. The number 123,000,000,000 in scientific notation is written as 1.23 x 1014 The number 0.00000508 in scientific notation is written as 5.08 x 10-6 ...
... express very large numbers. This method is called scientific notation. Scientific Notation is based on powers of the base number 10. The number 123,000,000,000 in scientific notation is written as 1.23 x 1014 The number 0.00000508 in scientific notation is written as 5.08 x 10-6 ...
Variables, expressions and statements
... Programmers generally choose names for their variables that are meaningful—they document what the variable is used for. Variable names can be arbitrarily long. They can contain both letters and numbers, but they have to begin with a letter. Although it is legal to use uppercase letters, by conventio ...
... Programmers generally choose names for their variables that are meaningful—they document what the variable is used for. Variable names can be arbitrarily long. They can contain both letters and numbers, but they have to begin with a letter. Although it is legal to use uppercase letters, by conventio ...
Frege, Boolos, and Logical Objects
... in case p = q. But if we use a modern-day predicate logic instead of a term logic, distinguish propositions from truth values, and allow the propositional variables ‘p’ and ‘q’ to range over propositions, something like the following principle governing truth values would be assertible for a modern- ...
... in case p = q. But if we use a modern-day predicate logic instead of a term logic, distinguish propositions from truth values, and allow the propositional variables ‘p’ and ‘q’ to range over propositions, something like the following principle governing truth values would be assertible for a modern- ...
Lecture Notes on Elements of Discrete Mathematics: Sets, Functions
... To summarize, logic is the study of reasoning. The British mathematician and philosopher George Boole (1815–1864) is the man who made logic mathematical. His book The Mathematical Analysis of Logic was published in 1847. Mathematical logic has been inspired by the search of formal system to distingu ...
... To summarize, logic is the study of reasoning. The British mathematician and philosopher George Boole (1815–1864) is the man who made logic mathematical. His book The Mathematical Analysis of Logic was published in 1847. Mathematical logic has been inspired by the search of formal system to distingu ...
Lecture 2
... A Boolean variable that can denote a proposition is sometimes called a propositional variable. The operator greater than (<) is a predicate (covered in Later). Predicates are not directly representable as propositions. Greater than can be regarded as a function of two numerical arguments and a Boole ...
... A Boolean variable that can denote a proposition is sometimes called a propositional variable. The operator greater than (<) is a predicate (covered in Later). Predicates are not directly representable as propositions. Greater than can be regarded as a function of two numerical arguments and a Boole ...
eprint_4_1049_36.doc
... The relations <, >, ≤ and ≥ are called inequalities in order to distinguish them from the relation = of equality. The reader is certainly familiar with the representation of the integers as points on a straight line, called the number line R, as shown in Fig. 11-1. ...
... The relations <, >, ≤ and ≥ are called inequalities in order to distinguish them from the relation = of equality. The reader is certainly familiar with the representation of the integers as points on a straight line, called the number line R, as shown in Fig. 11-1. ...
The Foundations
... s1 can be represented as P(y, min(x,3)) we call any expression that can be put on the argument position of an atomic proposition a term Obviously, constants and variables are terms; moreover,if f is a function of arity n, and t1,...tn are n terms, then so is f(t1,...,tn). Transparency No. 1-25 ...
... s1 can be represented as P(y, min(x,3)) we call any expression that can be put on the argument position of an atomic proposition a term Obviously, constants and variables are terms; moreover,if f is a function of arity n, and t1,...tn are n terms, then so is f(t1,...,tn). Transparency No. 1-25 ...
pdf format
... Ordinal addition can also be characterized in terms of concatenation of well-orderings. Let (X, <) and (Y, <0 ) be two well-ordered sets, and define their concatenation to be the well-ordering which consists of ({0} × X) ∪ ({1} × Y ) with the lexicographic ordering. Then we have: Theorem 20 α + β is ...
... Ordinal addition can also be characterized in terms of concatenation of well-orderings. Let (X, <) and (Y, <0 ) be two well-ordered sets, and define their concatenation to be the well-ordering which consists of ({0} × X) ∪ ({1} × Y ) with the lexicographic ordering. Then we have: Theorem 20 α + β is ...
Principia Mathematica

The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913. In 1927, it appeared in a second edition with an important Introduction To the Second Edition, an Appendix A that replaced ✸9 and an all-new Appendix C.PM, as it is often abbreviated, was an attempt to describe a set of axioms and inference rules in symbolic logic from which all mathematical truths could in principle be proven. As such, this ambitious project is of great importance in the history of mathematics and philosophy, being one of the foremost products of the belief that such an undertaking may be achievable. However, in 1931, Gödel's incompleteness theorem proved definitively that PM, and in fact any other attempt, could never achieve this lofty goal; that is, for any set of axioms and inference rules proposed to encapsulate mathematics, either the system must be inconsistent, or there must in fact be some truths of mathematics which could not be deduced from them.One of the main inspirations and motivations for PM was the earlier work of Gottlob Frege on logic, which Russell discovered allowed for the construction of paradoxical sets. PM sought to avoid this problem by ruling out the unrestricted creation of arbitrary sets. This was achieved by replacing the notion of a general set with the notion of a hierarchy of sets of different 'types', a set of a certain type only allowed to contain sets of strictly lower types. Contemporary mathematics, however, avoids paradoxes such as Russell's in less unwieldy ways, such as the system of Zermelo–Fraenkel set theory.PM is not to be confused with Russell's 1903 Principles of Mathematics. PM states: ""The present work was originally intended by us to be comprised in a second volume of Principles of Mathematics... But as we advanced, it became increasingly evident that the subject is a very much larger one than we had supposed; moreover on many fundamental questions which had been left obscure and doubtful in the former work, we have now arrived at what we believe to be satisfactory solutions.""The Modern Library placed it 23rd in a list of the top 100 English-language nonfiction books of the twentieth century.













![arXiv:math/9205211v1 [math.HO] 1 May 1992](http://s1.studyres.com/store/data/017806193_1-68d48c35d33f53708478382611422518-300x300.png)