MODIFIED MERSENNE NUMBERS AND PRIMES Several thousand
... That is , if one takes two to a prime power p and subtracts one from the result , one will generate a higher prime. Mersenne thought this might be true for all prime powers of two, but his conjecture was proven wrong as already shown by 211-1=2047=23·89. The prime powers p=13,17, and 19 work again, ...
... That is , if one takes two to a prime power p and subtracts one from the result , one will generate a higher prime. Mersenne thought this might be true for all prime powers of two, but his conjecture was proven wrong as already shown by 211-1=2047=23·89. The prime powers p=13,17, and 19 work again, ...
SOML MEET 2 NAME: ______ EVENT 3 TEAM: ______ Number
... at the end of the product. Since the product is of prime numbers, there is only one way to get a 10, from 2 and 5. So, there will be only 1 zero at the end of the product. ANS: __1 zero__ ...
... at the end of the product. Since the product is of prime numbers, there is only one way to get a 10, from 2 and 5. So, there will be only 1 zero at the end of the product. ANS: __1 zero__ ...
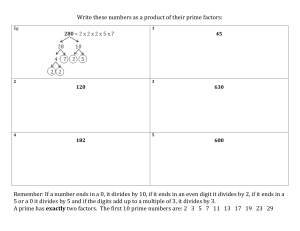
Prime factorisation
... A prime number is a number that has exactly two factors. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, etc. Note that 1 is not classed as a prime number (as it uniquely has just 1 factor). Any whole number can be written as a product of prime numbers. We can find the prime factorisatio ...
... A prime number is a number that has exactly two factors. The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, etc. Note that 1 is not classed as a prime number (as it uniquely has just 1 factor). Any whole number can be written as a product of prime numbers. We can find the prime factorisatio ...
Primes and Squares Challenge
... Try to find a rule which helps you to predict which prime numbers can be written as the sum of two square numbers and which cannot. ...
... Try to find a rule which helps you to predict which prime numbers can be written as the sum of two square numbers and which cannot. ...
Skill: Prime Factorization
... 27. The GCF of two numbers is 850. Neither number is divisible by the other. What is the smallest that these two numbers could be? ...
... 27. The GCF of two numbers is 850. Neither number is divisible by the other. What is the smallest that these two numbers could be? ...
Prime number theorem
In number theory, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée-Poussin in 1896 using ideas introduced by Bernhard Riemann (in particular, the Riemann zeta function).The first such distribution found is π(N) ~ N / log(N), where π(N) is the prime-counting function and log(N) is the natural logarithm of N. This means that for large enough N, the probability that a random integer not greater than N is prime is very close to 1 / log(N). Consequently, a random integer with at most 2n digits (for large enough n) is about half as likely to be prime as a random integer with at most n digits. For example, among the positive integers of at most 1000 digits, about one in 2300 is prime (log(101000) ≈ 2302.6), whereas among positive integers of at most 2000 digits, about one in 4600 is prime (log(102000) ≈ 4605.2). In other words, the average gap between consecutive prime numbers among the first N integers is roughly log(N).