Week 15
... If there is 1 odd number and 3 even numbers, there are only four possible selections, namely, {1, 2, 4, 6}, {3, 2, 4, 6}, {5, 2, 4, 6}, and {7, 2, 4, 6}. Once the odd number is selected, the 3 even numbers, {2, 4, 6}, must be selected. If there are 3 odd numbers and 1 even number, there are twelve p ...
... If there is 1 odd number and 3 even numbers, there are only four possible selections, namely, {1, 2, 4, 6}, {3, 2, 4, 6}, {5, 2, 4, 6}, and {7, 2, 4, 6}. Once the odd number is selected, the 3 even numbers, {2, 4, 6}, must be selected. If there are 3 odd numbers and 1 even number, there are twelve p ...
Document
... If there was some right triangle of integers that had an area equal to a square there would be another triangle less than it which has the same property. If there were a second less than the first which had the same property there would be by similar reasoning a third less than the second which had ...
... If there was some right triangle of integers that had an area equal to a square there would be another triangle less than it which has the same property. If there were a second less than the first which had the same property there would be by similar reasoning a third less than the second which had ...
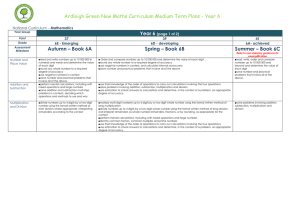
Year 6
... and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context ■perform mental calculations, including with mixed operations and large numbers ■identify common factors, common multiples and prime numbers ■use their knowledge of the order of operations ...
... and interpret remainders as whole number remainders, fractions, or by rounding, as appropriate for the context ■perform mental calculations, including with mixed operations and large numbers ■identify common factors, common multiples and prime numbers ■use their knowledge of the order of operations ...
Randomized local-spin mutual exclusion
... • After incurring O(log Δ) RMRs on a node, compete for the MX lock. Then spin trying to capture node lock. • In addition to randomized and deterministic promotion, an exiting process promotes also the process that holds the MX lock, if any. ...
... • After incurring O(log Δ) RMRs on a node, compete for the MX lock. Then spin trying to capture node lock. • In addition to randomized and deterministic promotion, an exiting process promotes also the process that holds the MX lock, if any. ...
Sieve of Eratosthenes

In mathematics, the sieve of Eratosthenes (Ancient Greek: κόσκινον Ἐρατοσθένους, kóskinon Eratosthénous), one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the multiples of 2.The multiples of a given prime are generated as a sequence of numbers starting from that prime, with constant difference between them that is equal to that prime. This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime.The sieve of Eratosthenes is one of the most efficient ways to find all of the smaller primes. It is named after Eratosthenes of Cyrene, a Greek mathematician; although none of his works have survived, the sieve was described and attributed to Eratosthenes in the Introduction to Arithmetic by Nicomachus.The sieve may be used to find primes in arithmetic progressions.