CS243: Discrete Structures Mathematical Proof Techniques
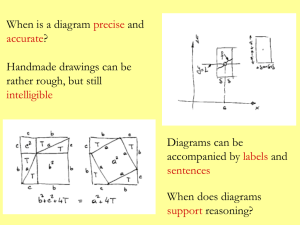
... Proof by cases: Exhaustively enumerate different possibilities, and prove the theorem for each case ...
... Proof by cases: Exhaustively enumerate different possibilities, and prove the theorem for each case ...
SOME IRRATIONAL NUMBERS Proposition 1. The square root of 2
... infinitude of primes. As he says, this is inevitably a proof by contradiction (unlike Euclid’s proof, which constructs new primes in a perfectly explicit way). The original statement is logically more complicated than what √ we actually prove in that it takes for granted that there is some real numb ...
... infinitude of primes. As he says, this is inevitably a proof by contradiction (unlike Euclid’s proof, which constructs new primes in a perfectly explicit way). The original statement is logically more complicated than what √ we actually prove in that it takes for granted that there is some real numb ...
Fractions don`t exist
... Proof. Suppose this is false, so let a be a point in the circle, not the centre. Then there is no point on the circumference nearest to a. This is absurd, so we have a contradiction. Therefore the only point inside a circle is its ...
... Proof. Suppose this is false, so let a be a point in the circle, not the centre. Then there is no point on the circumference nearest to a. This is absurd, so we have a contradiction. Therefore the only point inside a circle is its ...
Methods of Proof
... Proof by Contradiction (properly) If 3n + 2 is odd then n is odd Theorem: If 3n+2 is odd then n is odd. Proof: We use a proof by contradiction. Assume that 3n+2 is odd and n is even. Then we can express n as 2k, where k is an integer. Therefore 3n+2 is then 6k+2, i.e. 2(3k+1), and this is an even n ...
... Proof by Contradiction (properly) If 3n + 2 is odd then n is odd Theorem: If 3n+2 is odd then n is odd. Proof: We use a proof by contradiction. Assume that 3n+2 is odd and n is even. Then we can express n as 2k, where k is an integer. Therefore 3n+2 is then 6k+2, i.e. 2(3k+1), and this is an even n ...
notes
... Intuitionistic logic is the basis of constructive mathematics. Constructive mathematics takes a much more conservative view of truth than classical mathematics. It is concerned less with truth than with provability. Its main proponents were Kronecker and Brouwer around the beginning of the last cent ...
... Intuitionistic logic is the basis of constructive mathematics. Constructive mathematics takes a much more conservative view of truth than classical mathematics. It is concerned less with truth than with provability. Its main proponents were Kronecker and Brouwer around the beginning of the last cent ...
Study Guide Unit Test2 with Sample Problems
... x, teacher(x) make_mistakes(x) x, god(x) ~make_mistakes(x) x, make_mistakes (x) ~ god (x) ...
... x, teacher(x) make_mistakes(x) x, god(x) ~make_mistakes(x) x, make_mistakes (x) ~ god (x) ...
Mathematical proof

In mathematics, a proof is a deductive argument for a mathematical statement. In the argument, other previously established statements, such as theorems, can be used. In principle, a proof can be traced back to self-evident or assumed statements, known as axioms. Proofs are examples of deductive reasoning and are distinguished from inductive or empirical arguments; a proof must demonstrate that a statement is always true (occasionally by listing all possible cases and showing that it holds in each), rather than enumerate many confirmatory cases. An unproved proposition that is believed true is known as a conjecture.Proofs employ logic but usually include some amount of natural language which usually admits some ambiguity. In fact, the vast majority of proofs in written mathematics can be considered as applications of rigorous informal logic. Purely formal proofs, written in symbolic language instead of natural language, are considered in proof theory. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice, quasi-empiricism in mathematics, and so-called folk mathematics (in both senses of that term). The philosophy of mathematics is concerned with the role of language and logic in proofs, and mathematics as a language.