Algebra 3 - Superceded eRiding website
... Main Teaching (2 lessons - possibly 3) Objective A In equation 5x + 4 = 2x + 31 x is a particular single value. What is it? Discuss method of solution. In the formula v = u + at v, u, a and t are variable values. If we know 3 values we can work out the fourth value. (What if we know 2 values). In th ...
... Main Teaching (2 lessons - possibly 3) Objective A In equation 5x + 4 = 2x + 31 x is a particular single value. What is it? Discuss method of solution. In the formula v = u + at v, u, a and t are variable values. If we know 3 values we can work out the fourth value. (What if we know 2 values). In th ...
CHAP10 Polynomials in Several Variables
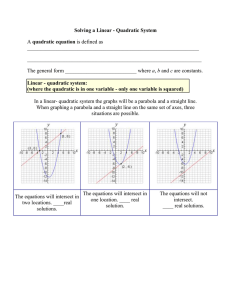
... Thus (x4 16)(x 1) = 0. This gives real solutions x = 1, 2. Substituting into the first equation gives the corresponding values of y. The solutions (x, y) are thus: (1, 15), (1, 15), (2, 2), (2, 2) N.B. There are no real solutions for y if x = 2. NOTE: A system of linear equations must eith ...
... Thus (x4 16)(x 1) = 0. This gives real solutions x = 1, 2. Substituting into the first equation gives the corresponding values of y. The solutions (x, y) are thus: (1, 15), (1, 15), (2, 2), (2, 2) N.B. There are no real solutions for y if x = 2. NOTE: A system of linear equations must eith ...
Gibb`s minimization principle for approximate solutions of scalar
... A BSTRACT. In this work we study variational properties of approximate solutions of scalar conservations laws. Solutions of this type are described by a kinetic equation which is similar to the kinetic representation of admissible weak solutions due to Lions-Perthame-Tadmor[12], but also retain smal ...
... A BSTRACT. In this work we study variational properties of approximate solutions of scalar conservations laws. Solutions of this type are described by a kinetic equation which is similar to the kinetic representation of admissible weak solutions due to Lions-Perthame-Tadmor[12], but also retain smal ...
9 - Houston ISD
... side, you must do to the other (what’s one number you can’t divide by? 0) so just call it the golden rule o When the coefficient is a fraction, multiply by the reciprocal (multiplicative inverse) Combine like terms on both sides of the equation to simplify expressions before solving *Address Unit ...
... side, you must do to the other (what’s one number you can’t divide by? 0) so just call it the golden rule o When the coefficient is a fraction, multiply by the reciprocal (multiplicative inverse) Combine like terms on both sides of the equation to simplify expressions before solving *Address Unit ...
3.2ss - Souderton Math
... 3.2 Solving Systems by Elimination Objective: Solve a system of two linear equations in two variables by elimination. Standard: 2.8.11.H. Select and use an appropriate strategy to solve systems of equations. ...
... 3.2 Solving Systems by Elimination Objective: Solve a system of two linear equations in two variables by elimination. Standard: 2.8.11.H. Select and use an appropriate strategy to solve systems of equations. ...