ahsge - Walker County Schools
... Purpose: This curriculum guide is a framework for standardized testing alignment and documentation of instruction. It contains a suggested sequencing guide. It is not inclusive of all possible instruction. Content standards are minimum; they are fundamental, but not exhaustive. This documentation sh ...
... Purpose: This curriculum guide is a framework for standardized testing alignment and documentation of instruction. It contains a suggested sequencing guide. It is not inclusive of all possible instruction. Content standards are minimum; they are fundamental, but not exhaustive. This documentation sh ...
Measuring Shapes in Geosketch
... simple geometric concept? • Why should we use Geometer’s Sketchpad as a tool to learn about Geometry? ...
... simple geometric concept? • Why should we use Geometer’s Sketchpad as a tool to learn about Geometry? ...
Graduation Test Review
... A street map is placed on a coordinate grid. The length of each square on the grid is 100 yards. Main Street is represented by the line y = −2 on the grid. • The coordinates of Chad’s business are (−5, 2). • The coordinates of Dwayne’s business are (−2,−6). Chad walks the SHORTEST distance from his ...
... A street map is placed on a coordinate grid. The length of each square on the grid is 100 yards. Main Street is represented by the line y = −2 on the grid. • The coordinates of Chad’s business are (−5, 2). • The coordinates of Dwayne’s business are (−2,−6). Chad walks the SHORTEST distance from his ...
2005 Mississippi Mu Alpha Theta Inter-School Test
... interval containing the probability that both A and B occur. ...
... interval containing the probability that both A and B occur. ...
Review Packet #12-16
... Identify the congruent triangles and name their corresponding congruent angles. ...
... Identify the congruent triangles and name their corresponding congruent angles. ...
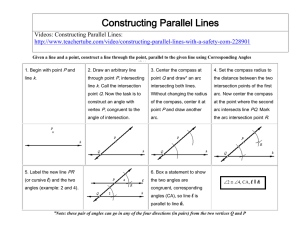
Construting parallel lines
... Do each Geometric Construction twice (using a compass and straight edge). Mark all new ANGLES, LINES, and congruent parts and box a statement describing the construction. Construct eight pairs of parallel line pairs, given a line and a point off the line. Using Converse of CAP (twice: one acute /. o ...
... Do each Geometric Construction twice (using a compass and straight edge). Mark all new ANGLES, LINES, and congruent parts and box a statement describing the construction. Construct eight pairs of parallel line pairs, given a line and a point off the line. Using Converse of CAP (twice: one acute /. o ...
Grade 4 Unit 5: Angle Measure and Plane Figures (4 weeks)
... • An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the two rays intersect the circle. An angle that turns through 1/360 of a circle is called a “one-degree angle,” and can be u ...
... • An angle is measured with reference to a circle with its center at the common endpoint of the rays, by considering the fraction of the circular arc between the points where the two rays intersect the circle. An angle that turns through 1/360 of a circle is called a “one-degree angle,” and can be u ...
2013年1月12日托福写作真题回忆
... Question 3: 60% of the players of a team score 5 points each during a basketball game, 30% of players score 1 point each, and 10% score 7 points each. What is the average number of points scored by the players of the team? Answer: 4 Explanation: n being the number of players, 60% of the players is . ...
... Question 3: 60% of the players of a team score 5 points each during a basketball game, 30% of players score 1 point each, and 10% score 7 points each. What is the average number of points scored by the players of the team? Answer: 4 Explanation: n being the number of players, 60% of the players is . ...
Line (geometry)
The notion of line or straight line was introduced by ancient mathematicians to represent straight objects (i.e., having no curvature) with negligible width and depth. Lines are an idealization of such objects. Until the seventeenth century, lines were defined in this manner: ""The [straight or curved] line is the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which […] will leave from its imaginary moving some vestige in length, exempt of any width. […] The straight line is that which is equally extended between its points""Euclid described a line as ""breadthless length"" which ""lies equally with respect to the points on itself""; he introduced several postulates as basic unprovable properties from which he constructed the geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of nineteenth century (such as non-Euclidean, projective and affine geometry).In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analytic geometry, a line in the plane is often defined as the set of points whose coordinates satisfy a given linear equation, but in a more abstract setting, such as incidence geometry, a line may be an independent object, distinct from the set of points which lie on it.When a geometry is described by a set of axioms, the notion of a line is usually left undefined (a so-called primitive object). The properties of lines are then determined by the axioms which refer to them. One advantage to this approach is the flexibility it gives to users of the geometry. Thus in differential geometry a line may be interpreted as a geodesic (shortest path between points), while in some projective geometries a line is a 2-dimensional vector space (all linear combinations of two independent vectors). This flexibility also extends beyond mathematics and, for example, permits physicists to think of the path of a light ray as being a line.A line segment is a part of a line that is bounded by two distinct end points and contains every point on the line between its end points. Depending on how the line segment is defined, either of the two end points may or may not be part of the line segment. Two or more line segments may have some of the same relationships as lines, such as being parallel, intersecting, or skew, but unlike lines they may be none of these, if they are coplanar and either do not intersect or are collinear.