The Nilpotent case. A Lie algebra is called “nilpotent” if there is an
... The group of all n × n upper triangular matrices with 1’s on the diagonal is nilpotent of degree n − 1. Motivations for studying nilpotent groups. They arise in the theory of distributions (subbundles of the tangent bundle), and hence in nonlinear control theory. They are the first case where Kirril ...
... The group of all n × n upper triangular matrices with 1’s on the diagonal is nilpotent of degree n − 1. Motivations for studying nilpotent groups. They arise in the theory of distributions (subbundles of the tangent bundle), and hence in nonlinear control theory. They are the first case where Kirril ...
Atom structures
... AC atom-canonical if (At A)+ is in V for every atomic A in V, or equivalently, if At V ⊆ Str V.4 AX atom-complex if every atomic algebra in V is isomorphic to a complex algebra over its atom structure. AO atom-corresponding if there is a set ∆ of first order sentences in the frame language such that ...
... AC atom-canonical if (At A)+ is in V for every atomic A in V, or equivalently, if At V ⊆ Str V.4 AX atom-complex if every atomic algebra in V is isomorphic to a complex algebra over its atom structure. AO atom-corresponding if there is a set ∆ of first order sentences in the frame language such that ...
Matrix Theory Review for Final Exam The final exam is Wednesday
... Eigenvalues and Eigenvectors Let A be an n by n matrix. Then an eigenvector of A is a nonzero vector x such that Ax and x are multiples of each other. In otherwords Ax = λx for some scalar λ. An eigenvalue of A is a scalar λ so that Ax = λx for some nonzero vector x. An eigenpair of A is a pair (λ, ...
... Eigenvalues and Eigenvectors Let A be an n by n matrix. Then an eigenvector of A is a nonzero vector x such that Ax and x are multiples of each other. In otherwords Ax = λx for some scalar λ. An eigenvalue of A is a scalar λ so that Ax = λx for some nonzero vector x. An eigenpair of A is a pair (λ, ...
Separation of Variables and the Computation of Fourier
... arrow and adding an arrow from vertex 0 to the bottom vertex of grading 1, we produce a Bratteli diagram. Consider a group algebra chain C[Gn ] > C[Gn−1 ] > · · · > C[G1 ] > C[G0 ] = C. To associate a Bratelli diagram to this chain we follow the language of [Ram97]. Let ρ be an irreducible represent ...
... arrow and adding an arrow from vertex 0 to the bottom vertex of grading 1, we produce a Bratteli diagram. Consider a group algebra chain C[Gn ] > C[Gn−1 ] > · · · > C[G1 ] > C[G0 ] = C. To associate a Bratelli diagram to this chain we follow the language of [Ram97]. Let ρ be an irreducible represent ...
Math 3121 Lecture 4 Sections 5
... ordinary addition modulo n (remainder when the sum is divided by n). Explain in class. • In class look at tables for ℤ2 ,ℤ3 ℤ4. • Note that ℤn is isomorphic to the nth roots of unity in the complex plane with multiplicative notation. Examples? ...
... ordinary addition modulo n (remainder when the sum is divided by n). Explain in class. • In class look at tables for ℤ2 ,ℤ3 ℤ4. • Note that ℤn is isomorphic to the nth roots of unity in the complex plane with multiplicative notation. Examples? ...
Math 3121 Abstract Algebra I
... ordinary addition modulo n (remainder when the sum is divided by n). Explain in class. • In class look at tables for ℤ2 ,ℤ3 ℤ4. • Note that ℤn is isomorphic to the nth roots of unity in the complex plane with multiplicative notation. Examples? ...
... ordinary addition modulo n (remainder when the sum is divided by n). Explain in class. • In class look at tables for ℤ2 ,ℤ3 ℤ4. • Note that ℤn is isomorphic to the nth roots of unity in the complex plane with multiplicative notation. Examples? ...
Projective p-adic representations of the K-rational geometric fundamental group (with G. Frey).
... Néron-Ogg-Shafarevich: A has to have good reduction everywhere, i.e. at all points of C. A second condition is that the fixed fields of (finite quotients of) the kernels of the ρ̃Vi ’s are regular extensions of F . Note that by using group theoretical methods it not difficult to find examples of ab ...
... Néron-Ogg-Shafarevich: A has to have good reduction everywhere, i.e. at all points of C. A second condition is that the fixed fields of (finite quotients of) the kernels of the ρ̃Vi ’s are regular extensions of F . Note that by using group theoretical methods it not difficult to find examples of ab ...
1. New Algebraic Tools for Classical Geometry
... objects. Our purpose here is to introduce powerful new mathematical tools for meeting that objective and developing new insights within a unified algebraic framework. In this and subsequent chapters we show how classical geometry fits neatly into the broader mathematical system of Geometric Algebra ...
... objects. Our purpose here is to introduce powerful new mathematical tools for meeting that objective and developing new insights within a unified algebraic framework. In this and subsequent chapters we show how classical geometry fits neatly into the broader mathematical system of Geometric Algebra ...
1 Groups
... nonzero real and complex numbers, respectively, are groups with respect to multiplication. 4. The set S 1 = {z ∈ C : |z| = 1} of complex numbers of modulus 1 is a group with respect to multiplication of complex numbers. 5. The set of invertible n × n matrices forms a group with respect to matrix mul ...
... nonzero real and complex numbers, respectively, are groups with respect to multiplication. 4. The set S 1 = {z ∈ C : |z| = 1} of complex numbers of modulus 1 is a group with respect to multiplication of complex numbers. 5. The set of invertible n × n matrices forms a group with respect to matrix mul ...
LIE-ADMISSIBLE ALGEBRAS AND THE VIRASORO
... We now show that σ is identically zero on W × W. If i 6= 0, then by (4) and (12) σ ([ei , e−i ], e0 ) = −2i σ (e0 , e0 ) = σ (ei , [e−i , e0 ]) = i σ (ei , e−i ) and hence σ (ei , e−i ) = −2σ (e0 , e0 ). For a j 6= 0 with i + j 6= 0, one has by (4) and (12) σ ([ei , ej ], e−(i+ j ) ) = −2( j − i )σ ...
... We now show that σ is identically zero on W × W. If i 6= 0, then by (4) and (12) σ ([ei , e−i ], e0 ) = −2i σ (e0 , e0 ) = σ (ei , [e−i , e0 ]) = i σ (ei , e−i ) and hence σ (ei , e−i ) = −2σ (e0 , e0 ). For a j 6= 0 with i + j 6= 0, one has by (4) and (12) σ ([ei , ej ], e−(i+ j ) ) = −2( j − i )σ ...
ABSTRACT ALGEBRA 1, LECTURE NOTES 5: HOMOMORPHISMS
... Definition 2.1. Let G be a group. I will use multiplicative notation for G. A subgroup of G is a subset S of G satisfying the properties: • the identity element 1 ∈ G is contained in S , • given two elements x, y ∈ S , their product xy in G is also contained in S , and • given an element x ∈ S , its ...
... Definition 2.1. Let G be a group. I will use multiplicative notation for G. A subgroup of G is a subset S of G satisfying the properties: • the identity element 1 ∈ G is contained in S , • given two elements x, y ∈ S , their product xy in G is also contained in S , and • given an element x ∈ S , its ...
as a PDF
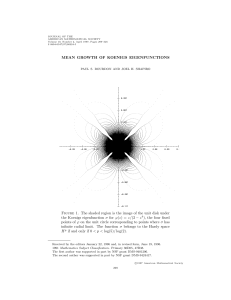
... ϕ0 (a) is always in the spectrum of Cϕ : H p → H p (the function z − a is easily seen to lie outside the range of the operator: see Proposition 3.3 for a proof in the case a = 0); thus, Fredholm theory guarantees that ϕ0 (a) must be an eigenvalue of Cϕ on H p . Since the Koenigs eigenfunction σ for ...
... ϕ0 (a) is always in the spectrum of Cϕ : H p → H p (the function z − a is easily seen to lie outside the range of the operator: see Proposition 3.3 for a proof in the case a = 0); thus, Fredholm theory guarantees that ϕ0 (a) must be an eigenvalue of Cϕ on H p . Since the Koenigs eigenfunction σ for ...
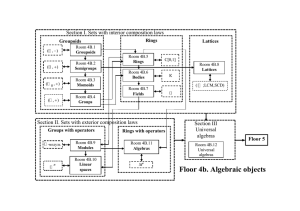
Section I. SETS WITH INTERIOR COMPOSITION LAWS
... Answer. This is the trivial group is the set with unique element е and operation , characterized by equality e e e . Example 4В.4 (task). Permutations group. Let М be a non empty finite set. The bijection from М to М is permutation. We determine an operation of superposition on the set Х of all ...
... Answer. This is the trivial group is the set with unique element е and operation , characterized by equality e e e . Example 4В.4 (task). Permutations group. Let М be a non empty finite set. The bijection from М to М is permutation. We determine an operation of superposition on the set Х of all ...
Let T be a locally finite rooted tree and G < Iso(T) be a
... Observations. 1. A weakly branch group has continuum many isometry types and cannot be small. 2. Let T be a locally finite rooted tree and G be a closed subgroup of Iso(T) with a small number of isometry types. Then for every m∈ω and h∈G there is some n∈ω and g∈G \ker πn such that g ker πn ⊆ h ker ...
... Observations. 1. A weakly branch group has continuum many isometry types and cannot be small. 2. Let T be a locally finite rooted tree and G be a closed subgroup of Iso(T) with a small number of isometry types. Then for every m∈ω and h∈G there is some n∈ω and g∈G \ker πn such that g ker πn ⊆ h ker ...
Semisimple algebras and Wedderburn`s theorem
... P U be a submodule of V .PLet I be a maximal subset of {1, . . . , k} such that ( i∈I Vi ) ∩ U = 0. Let W = i∈I Vi . We claim that W + U = V . If not, since V is a sum of the submodules Vi , there exists j ∈ {1, . . . , k} such that Vj is not contained in U + W . Then Vj ∩ (U + W ) is a submodule of ...
... P U be a submodule of V .PLet I be a maximal subset of {1, . . . , k} such that ( i∈I Vi ) ∩ U = 0. Let W = i∈I Vi . We claim that W + U = V . If not, since V is a sum of the submodules Vi , there exists j ∈ {1, . . . , k} such that Vj is not contained in U + W . Then Vj ∩ (U + W ) is a submodule of ...
Banach Spaces
... Proof: Let U be an open subset of X, and let T x ∈ T U, so that x ∈ Bǫ (x) ⊆ U. We will show that T B1 (0) contains a ball Br (0), from which follows that T x ∈ Brǫ (T x) = T x + ǫBr (0) ⊆ T x + ǫT B1 (0) = T Bǫ (x) ⊆ T U proving that T U is an open set. Let F = T B1 (0), and suppose that it does no ...
... Proof: Let U be an open subset of X, and let T x ∈ T U, so that x ∈ Bǫ (x) ⊆ U. We will show that T B1 (0) contains a ball Br (0), from which follows that T x ∈ Brǫ (T x) = T x + ǫBr (0) ⊆ T x + ǫT B1 (0) = T Bǫ (x) ⊆ T U proving that T U is an open set. Let F = T B1 (0), and suppose that it does no ...
LECTURES ON SYMPLECTIC REFLECTION ALGEBRAS 2. Algebras of Crawley-Boevey and Holland
... Problem 2.7. Show that if gr C⟨x, y⟩#Γ/(xy − yx − c) = C[x, y]#Γ, then c lies in the center of CΓ (that is equal to (CΓ)Γ , where the invariants are taken with respect to the adjoint action). For c ∈ (CΓ)Γ we set Hc := C⟨x, y⟩#Γ/(xy − yx − c). This is an algebra introduced by Crawley-Boevey and Holl ...
... Problem 2.7. Show that if gr C⟨x, y⟩#Γ/(xy − yx − c) = C[x, y]#Γ, then c lies in the center of CΓ (that is equal to (CΓ)Γ , where the invariants are taken with respect to the adjoint action). For c ∈ (CΓ)Γ we set Hc := C⟨x, y⟩#Γ/(xy − yx − c). This is an algebra introduced by Crawley-Boevey and Holl ...
Homework #3 Solutions (due 9/26/06)
... 3.5 Claim: Let ϕ : G → G0 be an isomorphism of groups. Then the inverse mapping ϕ−1 : G0 → G is also an isomorphism. Proof. Since ϕ : G → G0 is an isomorphism, in particular it is a bijection, and so the inverse mapping ϕ−1 : G0 → G exists and is also a bijection. So we only need to prove that ϕ−1 i ...
... 3.5 Claim: Let ϕ : G → G0 be an isomorphism of groups. Then the inverse mapping ϕ−1 : G0 → G is also an isomorphism. Proof. Since ϕ : G → G0 is an isomorphism, in particular it is a bijection, and so the inverse mapping ϕ−1 : G0 → G exists and is also a bijection. So we only need to prove that ϕ−1 i ...
3: Cross product - Harvard Mathematics Department
... Again, we do not have to prove anything since we have just defined volume and orientation. Let us still see why this fits with with our intuition about volume. The value h = |~u · ~n|/|~n| is the height of the parallelepiped if ~n = (~v × w) ~ is a normal vector to the ground parallelogram of area A ...
... Again, we do not have to prove anything since we have just defined volume and orientation. Let us still see why this fits with with our intuition about volume. The value h = |~u · ~n|/|~n| is the height of the parallelepiped if ~n = (~v × w) ~ is a normal vector to the ground parallelogram of area A ...
CHARACTERS OF FINITE GROUPS. As usual we consider a
... be the decomposition into simple modules. The characters χi = χSi are called irreducible characters. By convention n1 = 1 and S1 is the trivial representation. The corresponding character χ1 is called principal character. A character of a one dimensional representation is called a linear character. ...
... be the decomposition into simple modules. The characters χi = χSi are called irreducible characters. By convention n1 = 1 and S1 is the trivial representation. The corresponding character χ1 is called principal character. A character of a one dimensional representation is called a linear character. ...
Bochner`s linearization theorem
... The investigations by Cartan [3] of automorphisms and general transformations of a domain in several complex variables into itself by means of complex analytic functions led to the following result: If a compact group of automorphisms has a fixed point then in suitably chosen local coordinates aroun ...
... The investigations by Cartan [3] of automorphisms and general transformations of a domain in several complex variables into itself by means of complex analytic functions led to the following result: If a compact group of automorphisms has a fixed point then in suitably chosen local coordinates aroun ...