A note on linear codes and nonassociative algebras obtained from
... In recent years, several classes of linear codes were obtained from skew-polynomial rings (also called Ore rings). Using this approach, self-dual codes with a better minimal distance for certain lengths than previously known were constructed: while the classical cyclic codes of length m over a finit ...
... In recent years, several classes of linear codes were obtained from skew-polynomial rings (also called Ore rings). Using this approach, self-dual codes with a better minimal distance for certain lengths than previously known were constructed: while the classical cyclic codes of length m over a finit ...
Math 231b Lecture 01 G. Quick 1. Lecture 1: Vector bundles We start
... • a topological space E = E(ξ) called the total space • a continuous π : E → B called the projection map, and • for each b ∈ B the structure of a vector space over the real numbers R in the set Eb := π −1 (b). 2) The family ξ is called a real vector bundle over B if these data are subject to the fol ...
... • a topological space E = E(ξ) called the total space • a continuous π : E → B called the projection map, and • for each b ∈ B the structure of a vector space over the real numbers R in the set Eb := π −1 (b). 2) The family ξ is called a real vector bundle over B if these data are subject to the fol ...
Bose, R.C. and J.N. Srivastava; (1963)Multidimensional partially balanced designs and their analysis, with applications to partially balanced factorial fractions."
... this treatment combination will be denoted by y(jl' j2' ••• , jm). Also we shall v7rite E[y(jl" j2" •• ·,jm)] ...
... this treatment combination will be denoted by y(jl' j2' ••• , jm). Also we shall v7rite E[y(jl" j2" •• ·,jm)] ...
Invariant differential operators 1. Derivatives of group actions: Lie
... • Appendix: brackets • Appendix: proof of Poincaré-Birkhoff-Witt We want an intrinsic approach to existence of differential operators invariant under group actions. The translation-invariant operators ∂/∂xi on Rn , and the rotation-invariant Laplacian on Rn are deceptivelyeasily proven invariant, a ...
... • Appendix: brackets • Appendix: proof of Poincaré-Birkhoff-Witt We want an intrinsic approach to existence of differential operators invariant under group actions. The translation-invariant operators ∂/∂xi on Rn , and the rotation-invariant Laplacian on Rn are deceptivelyeasily proven invariant, a ...
x+y
... basic assumptions from which it is possible to deduce the rules. The most common postulates are as follows though not all apply to boolean algebra. • Closure Postulate: – A set S is closed with respect to a binary operator if, for every pair of elements of S, the binary operator specifies a rule for ...
... basic assumptions from which it is possible to deduce the rules. The most common postulates are as follows though not all apply to boolean algebra. • Closure Postulate: – A set S is closed with respect to a binary operator if, for every pair of elements of S, the binary operator specifies a rule for ...
SUBGROUPS OF VECTOR SPACES In what follows, finite
... In what follows, finite dimensional real vector spaces are always endowed with their usual topology, i.e., the topology induced from an arbitrary norm (or, equivalently, the topology induced from the Euclidean topology of Rn by an arbitrary choice of basis). Also, vector spaces are always endowed wi ...
... In what follows, finite dimensional real vector spaces are always endowed with their usual topology, i.e., the topology induced from an arbitrary norm (or, equivalently, the topology induced from the Euclidean topology of Rn by an arbitrary choice of basis). Also, vector spaces are always endowed wi ...
LECTURES ON SYMPLECTIC REFLECTION ALGEBRAS 7. Hochschild cohomology and deformations
... A0 . Definitely, if A is a graded deformation of A0 over S(P ), then A/AP 2 is a 1st order deformation of A0 . So understanding 1st order deformation is the 1st step in understanding deformations over S(P ). In what follows we will always assume that the degree of P is 2. We denote the product on A0 ...
... A0 . Definitely, if A is a graded deformation of A0 over S(P ), then A/AP 2 is a 1st order deformation of A0 . So understanding 1st order deformation is the 1st step in understanding deformations over S(P ). In what follows we will always assume that the degree of P is 2. We denote the product on A0 ...
Numerical multilinear algebra: From matrices to tensors
... Conditioning of multilinear systems (GV Chapter 3) Unsymmetric eigenvalue problem for hypermatrices (GV Chapter 7) Symmetric eigenvalue problem for hypermatrices (GV Chapter 8) Regularization of tensor approximation problems (GV Chapter 12) ...
... Conditioning of multilinear systems (GV Chapter 3) Unsymmetric eigenvalue problem for hypermatrices (GV Chapter 7) Symmetric eigenvalue problem for hypermatrices (GV Chapter 8) Regularization of tensor approximation problems (GV Chapter 12) ...
Lecture-6
... In a string variable • Numbers are stored as an array • A one-line string is a row vector Number of elements in vector is number of ...
... In a string variable • Numbers are stored as an array • A one-line string is a row vector Number of elements in vector is number of ...
19. Basis and Dimension
... S, which contradicts the assumption that S is linearly independent. Then for every i, ci = di . Next, we would like to establish a method for determining whether a collection of vectors forms a basis for Rn . But first, we need to show that any two bases for a finite-dimensional vector space has the ...
... S, which contradicts the assumption that S is linearly independent. Then for every i, ci = di . Next, we would like to establish a method for determining whether a collection of vectors forms a basis for Rn . But first, we need to show that any two bases for a finite-dimensional vector space has the ...
Representing the Simple Linear Regression Model as a Matrix
... Note 1: The inner product of two vectors is a number! Note 2: vT u uT v Orthogonal: Vectors v and u are orthogonal if vT u 0 . The geometrical interpretation is that the vectors are perpendicular. Orthogonality of vectors plays a big role in linear models. Length of a Vector: The length of vecto ...
... Note 1: The inner product of two vectors is a number! Note 2: vT u uT v Orthogonal: Vectors v and u are orthogonal if vT u 0 . The geometrical interpretation is that the vectors are perpendicular. Orthogonality of vectors plays a big role in linear models. Length of a Vector: The length of vecto ...
The Tangent Bundle - LSU Mathematics
... Given a smooth n-dimensional manifold M and x ∈ M , we see that a tangent vector in the tangent space at x should give rise to a ∼-equivalence class of chart vectors. We can reverse the procedure and define a tangent vector at x to be a ∼-class of chart vectors. Definition 2.1 Let M be an n-dimensi ...
... Given a smooth n-dimensional manifold M and x ∈ M , we see that a tangent vector in the tangent space at x should give rise to a ∼-equivalence class of chart vectors. We can reverse the procedure and define a tangent vector at x to be a ∼-class of chart vectors. Definition 2.1 Let M be an n-dimensi ...
Complex inner products
... each eigenvalue λj of A, choose an orthonormal (real) basis Bj of the eigenspace corresponding to λj . Let the columns of S be all these basis vectors in B1 , . . . , Bk . By b) this will make n columns. Then S ∗ AS is diagonal and by part c), S is orthogonal. I will now give an alternative proof wh ...
... each eigenvalue λj of A, choose an orthonormal (real) basis Bj of the eigenspace corresponding to λj . Let the columns of S be all these basis vectors in B1 , . . . , Bk . By b) this will make n columns. Then S ∗ AS is diagonal and by part c), S is orthogonal. I will now give an alternative proof wh ...
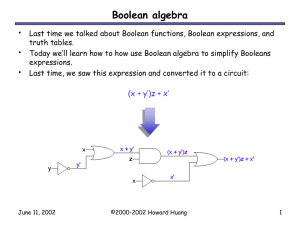
Boolean Algebra
... We can build complex functions from just the basic Boolean values “true” and “false,” and the operations AND, OR and NOT. Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expr ...
... We can build complex functions from just the basic Boolean values “true” and “false,” and the operations AND, OR and NOT. Any Boolean expression can be implemented with a circuit, which uses primitive logic gates to compute products, sums and complements. We saw two ways to prove equivalence of expr ...
Notes
... work to compute A−1 B using the backslash operator is O(n3 +n2 p)5 . Because matrix multiplication is associative, (AB)C and A(BC) are mathematically equivalent; but they can have very different performance depending on the matrix sizes. For example, if x, y, z ∈ Rn are three vectors (n × 1 matrices ...
... work to compute A−1 B using the backslash operator is O(n3 +n2 p)5 . Because matrix multiplication is associative, (AB)C and A(BC) are mathematically equivalent; but they can have very different performance depending on the matrix sizes. For example, if x, y, z ∈ Rn are three vectors (n × 1 matrices ...
CHAPTER 4 REVIEW 1. Finite dimensional vector spaces Any finite
... 4. Linear dependence and independence Proposition 4.1. A set of vectors S = {v1 , · · · , vn } is linearly dependent if and only if some vk can be expressed as a linear combination of the other vectors in S. Remark 4.2. In the textbook, the author proved that S = {v1 , · · · , vn } is linearly depen ...
... 4. Linear dependence and independence Proposition 4.1. A set of vectors S = {v1 , · · · , vn } is linearly dependent if and only if some vk can be expressed as a linear combination of the other vectors in S. Remark 4.2. In the textbook, the author proved that S = {v1 , · · · , vn } is linearly depen ...
8. Group algebras and Hecke algebras
... By determining which εH (hgi ) εH equal to each other each other we may write out the product as unique linear combination of Hecke basis elements. We summarize this discussion as the following. Proposition 8.5 The Hecke algebra is an associative algebra with basis εH hj εH , in 1-1 correspondence t ...
... By determining which εH (hgi ) εH equal to each other each other we may write out the product as unique linear combination of Hecke basis elements. We summarize this discussion as the following. Proposition 8.5 The Hecke algebra is an associative algebra with basis εH hj εH , in 1-1 correspondence t ...
EXTERIOR POWERS 1. Introduction Let R be a commutative ring
... Let R be a commutative ring. Unless indicated otherwise, all modules are R-modules and all tensor products are taken over R, so we abbreviate ⊗R to ⊗. A bilinear function out of M1 × M2 turns into a linear function out of the tensor product M1 ⊗ M2 . In a similar way, a multilinear function out of M ...
... Let R be a commutative ring. Unless indicated otherwise, all modules are R-modules and all tensor products are taken over R, so we abbreviate ⊗R to ⊗. A bilinear function out of M1 × M2 turns into a linear function out of the tensor product M1 ⊗ M2 . In a similar way, a multilinear function out of M ...
2. HARMONIC ANALYSIS ON COMPACT
... These notes recall some general facts about Fourier analysis on a compact group K. They will be applied eventually to compact Lie groups, particularly to the maximal compact subgroups of real reductive Lie groups. But much of the early material makes no use of the Lie group structure, so I’ll work w ...
... These notes recall some general facts about Fourier analysis on a compact group K. They will be applied eventually to compact Lie groups, particularly to the maximal compact subgroups of real reductive Lie groups. But much of the early material makes no use of the Lie group structure, so I’ll work w ...
Exterior algebra

In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogs. The exterior product of two vectors u and v, denoted by u ∧ v, is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of u ∧ v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. Like the cross product, the exterior product is anticommutative, meaning that u ∧ v = −(v ∧ u) for all vectors u and v. One way to visualize a bivector is as a family of parallelograms all lying in the same plane, having the same area, and with the same orientation of their boundaries—a choice of clockwise or counterclockwise.When regarded in this manner, the exterior product of two vectors is called a 2-blade. More generally, the exterior product of any number k of vectors can be defined and is sometimes called a k-blade. It lives in a space known as the kth exterior power. The magnitude of the resulting k-blade is the volume of the k-dimensional parallelotope whose edges are the given vectors, just as the magnitude of the scalar triple product of vectors in three dimensions gives the volume of the parallelepiped generated by those vectors.The exterior algebra, or Grassmann algebra after Hermann Grassmann, is the algebraic system whose product is the exterior product. The exterior algebra provides an algebraic setting in which to answer geometric questions. For instance, blades have a concrete geometric interpretation, and objects in the exterior algebra can be manipulated according to a set of unambiguous rules. The exterior algebra contains objects that are not just k-blades, but sums of k-blades; such a sum is called a k-vector. The k-blades, because they are simple products of vectors, are called the simple elements of the algebra. The rank of any k-vector is defined to be the smallest number of simple elements of which it is a sum. The exterior product extends to the full exterior algebra, so that it makes sense to multiply any two elements of the algebra. Equipped with this product, the exterior algebra is an associative algebra, which means that α ∧ (β ∧ γ) = (α ∧ β) ∧ γ for any elements α, β, γ. The k-vectors have degree k, meaning that they are sums of products of k vectors. When elements of different degrees are multiplied, the degrees add like multiplication of polynomials. This means that the exterior algebra is a graded algebra.The definition of the exterior algebra makes sense for spaces not just of geometric vectors, but of other vector-like objects such as vector fields or functions. In full generality, the exterior algebra can be defined for modules over a commutative ring, and for other structures of interest in abstract algebra. It is one of these more general constructions where the exterior algebra finds one of its most important applications, where it appears as the algebra of differential forms that is fundamental in areas that use differential geometry. Differential forms are mathematical objects that represent infinitesimal areas of infinitesimal parallelograms (and higher-dimensional bodies), and so can be integrated over surfaces and higher dimensional manifolds in a way that generalizes the line integrals from calculus. The exterior algebra also has many algebraic properties that make it a convenient tool in algebra itself. The association of the exterior algebra to a vector space is a type of functor on vector spaces, which means that it is compatible in a certain way with linear transformations of vector spaces. The exterior algebra is one example of a bialgebra, meaning that its dual space also possesses a product, and this dual product is compatible with the exterior product. This dual algebra is precisely the algebra of alternating multilinear forms, and the pairing between the exterior algebra and its dual is given by the interior product.