
Vector space, Independence, Basis, Dimension, Rank
... Dependence of two vectors. Define vectors v1 , v2 in R2 to be dependent provided they are not independent. This means one of v1 , v2 is the zero vector or else v1 and v2 lie along the same line: the two vectors cannot form a parallelogram. Algebraic detection of dependence is by failure of the indep ...
... Dependence of two vectors. Define vectors v1 , v2 in R2 to be dependent provided they are not independent. This means one of v1 , v2 is the zero vector or else v1 and v2 lie along the same line: the two vectors cannot form a parallelogram. Algebraic detection of dependence is by failure of the indep ...
8
... Definition (Linearly independent): A set of vectors {~v1 , · · · , ~vk } in vector space V is said to be linearly independent if the vector equation c1~v1 + c2 v~2 + · · · + ck~vk = ~0 has only the trivial solution: c1 = 0, · · · , ck = 0. (Linearly dependent): The set {~v1 , · · · , ~vk } is linear ...
... Definition (Linearly independent): A set of vectors {~v1 , · · · , ~vk } in vector space V is said to be linearly independent if the vector equation c1~v1 + c2 v~2 + · · · + ck~vk = ~0 has only the trivial solution: c1 = 0, · · · , ck = 0. (Linearly dependent): The set {~v1 , · · · , ~vk } is linear ...
On zero product determined algebras
... Let K be a commutative ring with identity.A K -algebra A is said to be zero product determined if for every K -bilinear ϕ having the property that ϕ(a1 , a2 ) = 0 whenever a1 a2 = 0, there is a K -linear ϕ̃ : A2 −→ Im ϕ such that ϕ(a1 , a2 ) = ϕ̃(a1 a2 ) for all a1 , a2 ∈ A. We provide a necessary a ...
... Let K be a commutative ring with identity.A K -algebra A is said to be zero product determined if for every K -bilinear ϕ having the property that ϕ(a1 , a2 ) = 0 whenever a1 a2 = 0, there is a K -linear ϕ̃ : A2 −→ Im ϕ such that ϕ(a1 , a2 ) = ϕ̃(a1 a2 ) for all a1 , a2 ∈ A. We provide a necessary a ...
Linear Vector Spaces
... the vector space of ordered pairs (x,y) with x ε X and y ε Y. Addition and scalar multiplication are defined by (x1,y1) + (x2,y2) = (x1+x2 , y1+y2) and α(x,y) = (αx,αy). We write Xn for the Cartesian product of X with itself n times. ...
... the vector space of ordered pairs (x,y) with x ε X and y ε Y. Addition and scalar multiplication are defined by (x1,y1) + (x2,y2) = (x1+x2 , y1+y2) and α(x,y) = (αx,αy). We write Xn for the Cartesian product of X with itself n times. ...
Ten ways to decompose a tensor
... L = [λi 0 i ] ∈ Rp×l , M = [µj 0 j ] ∈ Rq×m , N = [νk 0 k ] ∈ Rr ×n , (L, M, N) · A := Jci 0 j 0 k 0 K ∈ Rp×q×r where ci 0 j 0 k 0 := ...
... L = [λi 0 i ] ∈ Rp×l , M = [µj 0 j ] ∈ Rq×m , N = [νk 0 k ] ∈ Rr ×n , (L, M, N) · A := Jci 0 j 0 k 0 K ∈ Rp×q×r where ci 0 j 0 k 0 := ...
Lecture 38: Unitary operators
... A linear map T : V −→ W preserves inner products if for all v, v0 ∈ V we have (T v|T v0 ) = (v|v0 ). In this case T is injective. If T is also bijective, then we say that T is an isomorphism of inner product spaces. In this case T −1 also preserves inner products. A co-ordinate system C : Fn −→ V is ...
... A linear map T : V −→ W preserves inner products if for all v, v0 ∈ V we have (T v|T v0 ) = (v|v0 ). In this case T is injective. If T is also bijective, then we say that T is an isomorphism of inner product spaces. In this case T −1 also preserves inner products. A co-ordinate system C : Fn −→ V is ...
3 Lie Groups
... Given a vector field V(p) on a manifold M, we have seen how we can (at least locally) produce integral curves of V using the vector exponential map. Each point p in the neighborhood of interest lies on exactly one such curve, and the velocity of the curve at that point is exactly the vector given by ...
... Given a vector field V(p) on a manifold M, we have seen how we can (at least locally) produce integral curves of V using the vector exponential map. Each point p in the neighborhood of interest lies on exactly one such curve, and the velocity of the curve at that point is exactly the vector given by ...
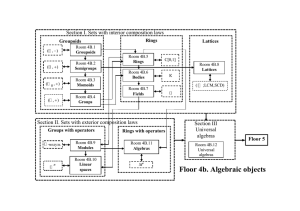
Section I. SETS WITH INTERIOR COMPOSITION LAWS
... We shall consider sets with algebraic structures. Its general notion is composition law. This is an operator, which maps a concrete quality (operation degree) of elements of the given set to an element of this set, for example, addition of numbers, sum of sets. Composition law can be interior and ex ...
... We shall consider sets with algebraic structures. Its general notion is composition law. This is an operator, which maps a concrete quality (operation degree) of elements of the given set to an element of this set, for example, addition of numbers, sum of sets. Composition law can be interior and ex ...
In algebra, a determinant is a function depending on
... which have the same determinant but are not similar. If A is a square n-by-n matrix with real or complex entries and if λ1,...,λn are the (complex) eigenvalues of A listed according to their algebraic multiplicities, then ...
... which have the same determinant but are not similar. If A is a square n-by-n matrix with real or complex entries and if λ1,...,λn are the (complex) eigenvalues of A listed according to their algebraic multiplicities, then ...
Inverse and Partition of Matrices and their Applications in Statistics
... Non-square matrices (m-by-n matrices for which m ≠ n) do not have an inverse. However, in some cases such a matrix may have a left inverse or right inverse. If A is m-by-n and the rank of A is equal to n, then A has a left inverse: an n-bym matrix B such that BA = I. If A has rank m, then it has a r ...
... Non-square matrices (m-by-n matrices for which m ≠ n) do not have an inverse. However, in some cases such a matrix may have a left inverse or right inverse. If A is m-by-n and the rank of A is equal to n, then A has a left inverse: an n-bym matrix B such that BA = I. If A has rank m, then it has a r ...
Section 15. The Product Topology on X × Y
... Note. As usual, we need to confirm that Munkres’ definition is meaningful and so we must verify that B is a basis or a topology. Since X is pen and Y is open, then X × Y ∈ B is open and part (1) of the definition of “basis” is satisfied. For part (2) of the definition, let B1 = U1 × V1 and B2 = U2 × ...
... Note. As usual, we need to confirm that Munkres’ definition is meaningful and so we must verify that B is a basis or a topology. Since X is pen and Y is open, then X × Y ∈ B is open and part (1) of the definition of “basis” is satisfied. For part (2) of the definition, let B1 = U1 × V1 and B2 = U2 × ...
Hecke algebras
... reductive group. For these, affine Weyl groups replace W . In the theory of Kazhdan and Lusztig, as well as in answering other questions in representation theory, it is important to know that the prime powers qα in the definition of the Hecke algebra may be replaced by variables. This is not so surp ...
... reductive group. For these, affine Weyl groups replace W . In the theory of Kazhdan and Lusztig, as well as in answering other questions in representation theory, it is important to know that the prime powers qα in the definition of the Hecke algebra may be replaced by variables. This is not so surp ...
PDF version of lecture with all slides
... Inner product represents a row matrix mul>plied by a column matrix. A row matrix can be mul>plied by a column matrix, in that order, only if they each have the same number of elements! In ...
... Inner product represents a row matrix mul>plied by a column matrix. A row matrix can be mul>plied by a column matrix, in that order, only if they each have the same number of elements! In ...
MTH 331 (sec 201) Syllabus Spring 2014 - MU BERT
... responsible for reading the text, working the exercises, coming to office hours for help when you’re stuck, and being aware of the dates for the major exams as they are announced. The TI-83 will be used in classroom demonstrations and is the recommended calculator, but you are free to use other bran ...
... responsible for reading the text, working the exercises, coming to office hours for help when you’re stuck, and being aware of the dates for the major exams as they are announced. The TI-83 will be used in classroom demonstrations and is the recommended calculator, but you are free to use other bran ...
arXiv:math/0005256v2 [math.QA] 21 Jun 2000
... we discuss complexes and give several examples; in this section we explain the constructions connected with simplicial modules and we describe the tensor product of complexes. Section 4 is a physical illustration of the fact that there is no natural tensor product of differential modules whereas the ...
... we discuss complexes and give several examples; in this section we explain the constructions connected with simplicial modules and we describe the tensor product of complexes. Section 4 is a physical illustration of the fact that there is no natural tensor product of differential modules whereas the ...
Exterior algebra

In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogs. The exterior product of two vectors u and v, denoted by u ∧ v, is called a bivector and lives in a space called the exterior square, a vector space that is distinct from the original space of vectors. The magnitude of u ∧ v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. Like the cross product, the exterior product is anticommutative, meaning that u ∧ v = −(v ∧ u) for all vectors u and v. One way to visualize a bivector is as a family of parallelograms all lying in the same plane, having the same area, and with the same orientation of their boundaries—a choice of clockwise or counterclockwise.When regarded in this manner, the exterior product of two vectors is called a 2-blade. More generally, the exterior product of any number k of vectors can be defined and is sometimes called a k-blade. It lives in a space known as the kth exterior power. The magnitude of the resulting k-blade is the volume of the k-dimensional parallelotope whose edges are the given vectors, just as the magnitude of the scalar triple product of vectors in three dimensions gives the volume of the parallelepiped generated by those vectors.The exterior algebra, or Grassmann algebra after Hermann Grassmann, is the algebraic system whose product is the exterior product. The exterior algebra provides an algebraic setting in which to answer geometric questions. For instance, blades have a concrete geometric interpretation, and objects in the exterior algebra can be manipulated according to a set of unambiguous rules. The exterior algebra contains objects that are not just k-blades, but sums of k-blades; such a sum is called a k-vector. The k-blades, because they are simple products of vectors, are called the simple elements of the algebra. The rank of any k-vector is defined to be the smallest number of simple elements of which it is a sum. The exterior product extends to the full exterior algebra, so that it makes sense to multiply any two elements of the algebra. Equipped with this product, the exterior algebra is an associative algebra, which means that α ∧ (β ∧ γ) = (α ∧ β) ∧ γ for any elements α, β, γ. The k-vectors have degree k, meaning that they are sums of products of k vectors. When elements of different degrees are multiplied, the degrees add like multiplication of polynomials. This means that the exterior algebra is a graded algebra.The definition of the exterior algebra makes sense for spaces not just of geometric vectors, but of other vector-like objects such as vector fields or functions. In full generality, the exterior algebra can be defined for modules over a commutative ring, and for other structures of interest in abstract algebra. It is one of these more general constructions where the exterior algebra finds one of its most important applications, where it appears as the algebra of differential forms that is fundamental in areas that use differential geometry. Differential forms are mathematical objects that represent infinitesimal areas of infinitesimal parallelograms (and higher-dimensional bodies), and so can be integrated over surfaces and higher dimensional manifolds in a way that generalizes the line integrals from calculus. The exterior algebra also has many algebraic properties that make it a convenient tool in algebra itself. The association of the exterior algebra to a vector space is a type of functor on vector spaces, which means that it is compatible in a certain way with linear transformations of vector spaces. The exterior algebra is one example of a bialgebra, meaning that its dual space also possesses a product, and this dual product is compatible with the exterior product. This dual algebra is precisely the algebra of alternating multilinear forms, and the pairing between the exterior algebra and its dual is given by the interior product.





















![arXiv:math/0005256v2 [math.QA] 21 Jun 2000](http://s1.studyres.com/store/data/017029559_1-d28b6a03fef36ff14eaa2fb575ab89be-300x300.png)