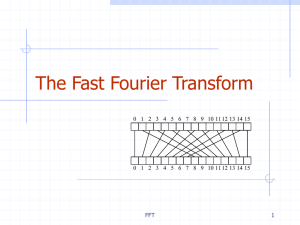
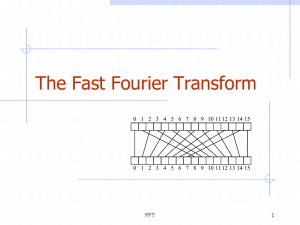
lecture notes as PDF
... If φ is a ring homomorphism from a ring R onto a ring S then the factor ring R/kerφ and the ring S are isomorphic by the map r + kerφ 7→ φ(r). We can use mappings to transfer a structure from an algebraic system to a set without structure. Given a ring R, a set S and a bijective map φ : R → S, we ca ...
... If φ is a ring homomorphism from a ring R onto a ring S then the factor ring R/kerφ and the ring S are isomorphic by the map r + kerφ 7→ φ(r). We can use mappings to transfer a structure from an algebraic system to a set without structure. Given a ring R, a set S and a bijective map φ : R → S, we ca ...
Solutions Sheet 8
... (b) If S is finitely generated over R by homogeneous elements of degree > 0, then Proj S is projective over R. Solution: Suppose that S is generated by homogeneous elements f0 , . . . , fn of degrees > 0 and homogeneous elements g1 , . . . , gm of degree 0, with m = 0 in the case (b). Let d be the l ...
... (b) If S is finitely generated over R by homogeneous elements of degree > 0, then Proj S is projective over R. Solution: Suppose that S is generated by homogeneous elements f0 , . . . , fn of degrees > 0 and homogeneous elements g1 , . . . , gm of degree 0, with m = 0 in the case (b). Let d be the l ...
Geometry of Cubic Polynomials - Exhibit
... The ellipse is flattened into a vertical ellipse, with the two outer vertices projecting to endpoints of an interval (line). In other words, the complex plane where this sphere exists is now vertical and directly above the real axis below in the other copy of the complex plane. If we were to stand o ...
... The ellipse is flattened into a vertical ellipse, with the two outer vertices projecting to endpoints of an interval (line). In other words, the complex plane where this sphere exists is now vertical and directly above the real axis below in the other copy of the complex plane. If we were to stand o ...
Field Theory and Galois Theory Part I: Ruler and
... root; call it alpha." Glance around nonchalantly, and nish him o with: \So I suppose R( ) is the eld you're looking for." Of course, you've been doing some quick thinking in the meantime. How to make up a eld? OK, you're pretending that 2 +1 = 0. Fine, that means 2 = ?1. Let's just work on add ...
... root; call it alpha." Glance around nonchalantly, and nish him o with: \So I suppose R( ) is the eld you're looking for." Of course, you've been doing some quick thinking in the meantime. How to make up a eld? OK, you're pretending that 2 +1 = 0. Fine, that means 2 = ?1. Let's just work on add ...
Homology With Local Coefficients
... Because of their importancein the work of Reidemeister,we shall discuss certainlocal systemsbased on the fundamentalgroup F of R. Let F' be an invariantsubgroupof F, and let {f = F/F1. Let 9' be an abelian group. Let G be the set of functionsfrom'Fto 1AJ.If two such functionsare added by addingfunct ...
... Because of their importancein the work of Reidemeister,we shall discuss certainlocal systemsbased on the fundamentalgroup F of R. Let F' be an invariantsubgroupof F, and let {f = F/F1. Let 9' be an abelian group. Let G be the set of functionsfrom'Fto 1AJ.If two such functionsare added by addingfunct ...