Full text
... 3: If k < b - 2 when b is prime, or k < the smallest prime factor of b when b is not prime, then, for any n and any set { }, there is an m such that none of wx\9 ..., mxk has the digit 1 among its n rightmost nonzero digits (a string of consecutive digits the last of which is the rightmost nonzero d ...
... 3: If k < b - 2 when b is prime, or k < the smallest prime factor of b when b is not prime, then, for any n and any set { }, there is an m such that none of wx\9 ..., mxk has the digit 1 among its n rightmost nonzero digits (a string of consecutive digits the last of which is the rightmost nonzero d ...
A polynomial time algorithm for the conjugacy
... groups [3]. Some very related results can also be seen in the work of Sale [11, 12], in which he shows that for a special class of the groups studied in this paper, the conjugacy length function is bounded from above by a linear function. Namely, for any two conjugate elements in these groups, there ...
... groups [3]. Some very related results can also be seen in the work of Sale [11, 12], in which he shows that for a special class of the groups studied in this paper, the conjugacy length function is bounded from above by a linear function. Namely, for any two conjugate elements in these groups, there ...
Group action
... remainder x mod p, which is of order 32. By Fermat little theorem, order of each element mod p divides p – 1, therefore p – 1 = 32k. (b) We shall need the following notion: Definition. Cyclotomic polynomial is. In other words, it is a monic polynomial that has simple roots which are “roots of 1 of d ...
... remainder x mod p, which is of order 32. By Fermat little theorem, order of each element mod p divides p – 1, therefore p – 1 = 32k. (b) We shall need the following notion: Definition. Cyclotomic polynomial is. In other words, it is a monic polynomial that has simple roots which are “roots of 1 of d ...
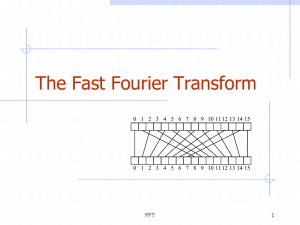
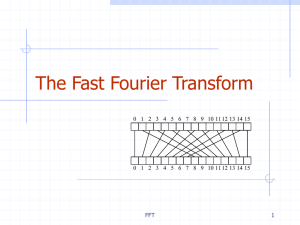
FFT - Personal Web Pages
... Given N-bit integers I and J, compute IJ. Assume: we can multiply words of O(log N) bits in constant time. Setup: Find a prime p=cn+1 that can be represented in one word, and set m=(log p)/3, so that we can view I and J as n-length vectors of m-bit words. Finding a primitive root of unity. ...
... Given N-bit integers I and J, compute IJ. Assume: we can multiply words of O(log N) bits in constant time. Setup: Find a prime p=cn+1 that can be represented in one word, and set m=(log p)/3, so that we can view I and J as n-length vectors of m-bit words. Finding a primitive root of unity. ...
1 Groups
... Example 8 Let G = hZ6 , +i, the set of numbers {0, 1, 2, 3, 4, 5} using addition modulo 6. It is straightforward to verify that this forms a group. Let H = h{0, 2, 4}, +i, with addition taken modulo 6. As a set, H ⊂ G, and it can be shown that H forms a group. Let K = h{0, 3}, +i, with addition take ...
... Example 8 Let G = hZ6 , +i, the set of numbers {0, 1, 2, 3, 4, 5} using addition modulo 6. It is straightforward to verify that this forms a group. Let H = h{0, 2, 4}, +i, with addition taken modulo 6. As a set, H ⊂ G, and it can be shown that H forms a group. Let K = h{0, 3}, +i, with addition take ...
Basic algorithms in number theory - Library
... of the number of “elemental operations” that the algorithm performs and is intended, in suitable contexts, to approximate the running time of actual computer programs implementing these algorithms. A formalization of these ideas requires precise definitions for “algorithm,” “input,” “output,” “cost, ...
... of the number of “elemental operations” that the algorithm performs and is intended, in suitable contexts, to approximate the running time of actual computer programs implementing these algorithms. A formalization of these ideas requires precise definitions for “algorithm,” “input,” “output,” “cost, ...
The Power of Depth 2 Circuits over Algebras
... address and answer this question. We assume that the algebra R is given in basis form i.e. we know an F-basis {e1 , . . . , ek } of R and we also know how ei e j can be expressed in terms of the basis elements, for all i and j. Since elements of a finite dimensional algebra, given in basis form, can ...
... address and answer this question. We assume that the algebra R is given in basis form i.e. we know an F-basis {e1 , . . . , ek } of R and we also know how ei e j can be expressed in terms of the basis elements, for all i and j. Since elements of a finite dimensional algebra, given in basis form, can ...
45 b a b a b a 2 = b a 2b a = 2 2 b c = b corb c = = b a
... iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. A finite continued fraction is similar, but the iteration/recursion is terminated after fin ...
... iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. A finite continued fraction is similar, but the iteration/recursion is terminated after fin ...
SOME TOPICS IN ALGEBRAIC EQUATIONS Institute of Numerical
... these notes, in particular, we can see some very useful applications of linear algebra to ancient problems of construction by compasses and ruler and then to the problem of solvability of algebraic equations by radicals. In this lecture course we go straightforwardly to some famous results of algebr ...
... these notes, in particular, we can see some very useful applications of linear algebra to ancient problems of construction by compasses and ruler and then to the problem of solvability of algebraic equations by radicals. In this lecture course we go straightforwardly to some famous results of algebr ...
Subfield-Compatible Polynomials over Finite Fields - Rose
... for all elements in E\K to 0 (assuming that E\K is nonempty). By Theorem 2.2, we can construct a polynomial f ∈ E[x] such that f (α) = g 0 (α) = g(α) ∈ L for all α ∈ K. Now had we chosen to map all the elements in E\K to 1 instead of 0, we would have obtained a different polynomial that when evaluat ...
... for all elements in E\K to 0 (assuming that E\K is nonempty). By Theorem 2.2, we can construct a polynomial f ∈ E[x] such that f (α) = g 0 (α) = g(α) ∈ L for all α ∈ K. Now had we chosen to map all the elements in E\K to 1 instead of 0, we would have obtained a different polynomial that when evaluat ...