Functional Programming and the Lambda Calculus
... The main (good) property of functional programming is referential transparency. Every expression denotes a single value. The value cannot be changed by evaluating an expression or by sharing it between different parts of the program. No references to global data; there is no global data. There are n ...
... The main (good) property of functional programming is referential transparency. Every expression denotes a single value. The value cannot be changed by evaluating an expression or by sharing it between different parts of the program. No references to global data; there is no global data. There are n ...
PPT
... (Direct Proof) If n is an odd natural number, then n2 is odd. Proof: An integer n is called odd if it is of the form n = 2k +1 for some integer k , then since we assumed n odd, we can write n = 2k +1. Squaring gives n2 = (2k +1)2 ...
... (Direct Proof) If n is an odd natural number, then n2 is odd. Proof: An integer n is called odd if it is of the form n = 2k +1 for some integer k , then since we assumed n odd, we can write n = 2k +1. Squaring gives n2 = (2k +1)2 ...
+x - WordPress.com
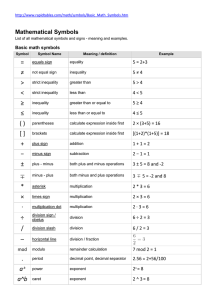
... http://www.rapidtables.com/math/symbols/Basic_Math_Symbols.htm function (cdf) ...
... http://www.rapidtables.com/math/symbols/Basic_Math_Symbols.htm function (cdf) ...



![[Ch 3, 4] Logic and Proofs (2) 1. Valid and Invalid Arguments (§2.3](http://s1.studyres.com/store/data/014954007_1-d36c768aba23f0b4aa633cb9a2a27ee2-300x300.png)