x - Stanford University
... As with predicates, functions can take in any number of arguments, but each function has a fixed arity. Functions evaluate to objects, not propositions. There is no syntactic way to distinguish functions and predicates; you'll have to look at how they're used. ...
... As with predicates, functions can take in any number of arguments, but each function has a fixed arity. Functions evaluate to objects, not propositions. There is no syntactic way to distinguish functions and predicates; you'll have to look at how they're used. ...
Proof Pearl: Defining Functions over Finite Sets
... We assume there already is a formalization of sets, with standard operations such as comprehension, union and intersection. In higher-order logic, this is trivial by the obvious representation of sets by predicates. We use standard mathematical notation with a few extensions. Type variables are writ ...
... We assume there already is a formalization of sets, with standard operations such as comprehension, union and intersection. In higher-order logic, this is trivial by the obvious representation of sets by predicates. We use standard mathematical notation with a few extensions. Type variables are writ ...
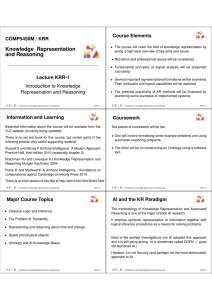
Knowledge Representation and Reasoning
... A tough issue that any AI reasoning system must confront is that of Tractability. A problem domain is intractable if it is not possible for a (conventional) computer program to solve it in ‘reasonable’ time (and with ‘reasonable’ use of other resources such as memory). Certain classes of logical pro ...
... A tough issue that any AI reasoning system must confront is that of Tractability. A problem domain is intractable if it is not possible for a (conventional) computer program to solve it in ‘reasonable’ time (and with ‘reasonable’ use of other resources such as memory). Certain classes of logical pro ...
FC §1.1, §1.2 - Mypage at Indiana University
... What we do with propositions is combine them with logical operators. A logical operator can be applied to one or more propositions to produce a new proposition. The truth value of the new proposition is completely determined by the operator and by the truth values of the propositions to which it is ...
... What we do with propositions is combine them with logical operators. A logical operator can be applied to one or more propositions to produce a new proposition. The truth value of the new proposition is completely determined by the operator and by the truth values of the propositions to which it is ...
Constructing Cut Free Sequent Systems With Context Restrictions
... rules which works uniformly for classical and intuitionistic logics. The rules so constructed are by construction sound and complete (in the presence of cut) and give rise to unlabelled sequent systems that are amenable to saturation under cuts between rules. In case the resulting rules fulfil our c ...
... rules which works uniformly for classical and intuitionistic logics. The rules so constructed are by construction sound and complete (in the presence of cut) and give rise to unlabelled sequent systems that are amenable to saturation under cuts between rules. In case the resulting rules fulfil our c ...
Modular Construction of Complete Coalgebraic Logics
... property which ensures that combined logics have the Hennessy-Milner property w.r.t. behavioural equivalence, that is, the logical equivalence of states coincides with behavioural equivalence. Since this property is present in all of the basic constructs and is preserved by each combination of const ...
... property which ensures that combined logics have the Hennessy-Milner property w.r.t. behavioural equivalence, that is, the logical equivalence of states coincides with behavioural equivalence. Since this property is present in all of the basic constructs and is preserved by each combination of const ...
Mathematical Logic Prof. Arindama Singh Department of
... implies B. This is also law of contradiction that we know. These are the only three axioms we are concerned with. First two, there is no negation symbol, but here we have the negations symbol. We will again assume the third one. These are the three axioms. When you say it is an axiom, it does not sa ...
... implies B. This is also law of contradiction that we know. These are the only three axioms we are concerned with. First two, there is no negation symbol, but here we have the negations symbol. We will again assume the third one. These are the three axioms. When you say it is an axiom, it does not sa ...
Handling Exceptions in nonmonotonic reasoning
... of this very simple defeasible axiomatic basis. Some argue that only g2 should be derived and others argue for splitting the expansions: one applying g1 and other applying g2 . Translating the example in Reiter’s default logic (according with Def. 2.4), it applies only the second rule, and this has ...
... of this very simple defeasible axiomatic basis. Some argue that only g2 should be derived and others argue for splitting the expansions: one applying g1 and other applying g2 . Translating the example in Reiter’s default logic (according with Def. 2.4), it applies only the second rule, and this has ...
Kripke completeness revisited
... possible worlds; All possible worlds are just all possible evaluations, the real world being represented by G and the other members of K representing possible worlds: The basis of the informal analysis which motivated these definitions is that a proposition is necessary if and only if it is true in ...
... possible worlds; All possible worlds are just all possible evaluations, the real world being represented by G and the other members of K representing possible worlds: The basis of the informal analysis which motivated these definitions is that a proposition is necessary if and only if it is true in ...
The Foundations
... Propositional logic (§1.1-1.2) (命題邏輯) Basic definitions (§1.1) Equivalence rules & derivations (§1.2) ...
... Propositional logic (§1.1-1.2) (命題邏輯) Basic definitions (§1.1) Equivalence rules & derivations (§1.2) ...
Document
... • To prove that every string x Expr satisfies a condition P(x), use structural induction: show that – P(a) is true – For every x and every y in Expr, if P(x) and P(y) are true, then P(x ◦ y) and P(x • y) are true – For every x Expr, if P(x) is true, then P(◊(x)) is true • In other words, show th ...
... • To prove that every string x Expr satisfies a condition P(x), use structural induction: show that – P(a) is true – For every x and every y in Expr, if P(x) and P(y) are true, then P(x ◦ y) and P(x • y) are true – For every x Expr, if P(x) is true, then P(◊(x)) is true • In other words, show th ...
Document
... • To prove that every string x Expr satisfies a condition P(x), use structural induction: show that – P(a) is true – For every x and every y in Expr, if P(x) and P(y) are true, then P(x ◦ y) and P(x • y) are true – For every x Expr, if P(x) is true, then P(◊(x)) is true • In other words, show th ...
... • To prove that every string x Expr satisfies a condition P(x), use structural induction: show that – P(a) is true – For every x and every y in Expr, if P(x) and P(y) are true, then P(x ◦ y) and P(x • y) are true – For every x Expr, if P(x) is true, then P(◊(x)) is true • In other words, show th ...
Nonmonotonic Reasoning - Computer Science Department
... outstrip all previously existing developments and present many new challenges which require non-traditional logics tailored to computer science. New problems suggested by computer science and artificial intelligence have led to an unprecedented multiplicity of intellectual challenges. As a result the ...
... outstrip all previously existing developments and present many new challenges which require non-traditional logics tailored to computer science. New problems suggested by computer science and artificial intelligence have led to an unprecedented multiplicity of intellectual challenges. As a result the ...
Propositional Proof Complexity An Introduction
... In order to talk about simulations between Frege systems over different languages, we must first fix a translation from formulas φ of one system to “equivalent” formulas φ0 of the other. There are two problems to overcome here: (1) First, something more than formal equivalence of φ and φ0 has to be ...
... In order to talk about simulations between Frege systems over different languages, we must first fix a translation from formulas φ of one system to “equivalent” formulas φ0 of the other. There are two problems to overcome here: (1) First, something more than formal equivalence of φ and φ0 has to be ...
The Computer Modelling of Mathematical Reasoning Alan Bundy
... theorem proving’ techniques could be readily brought into a Resolution framework, and how this helped us to relate the various techniques – creating coherence from confusion. In order to achieve this goal I have taken strong historical liberties in my descriptions of the work of Boyer and Moore, Gel ...
... theorem proving’ techniques could be readily brought into a Resolution framework, and how this helped us to relate the various techniques – creating coherence from confusion. In order to achieve this goal I have taken strong historical liberties in my descriptions of the work of Boyer and Moore, Gel ...
Written
... This relation is a partial ordering relation. The relation is reflexive because x(xN+ x=3nx) when n=0. The relation is antisymmetric because n cannot be negative or fractional, so for any element (x,y) we know xy, and there is no way to pair that element with another element where x
... This relation is a partial ordering relation. The relation is reflexive because x(xN+ x=3nx) when n=0. The relation is antisymmetric because n cannot be negative or fractional, so for any element (x,y) we know xy, and there is no way to pair that element with another element where x
Hilbert`s Program Then and Now - Philsci
... In about 1920, Hilbert came to reject Russell’s logicist solution to the consistency problem for arithmetic, mainly for the reason that the axiom of reducibility cannot be accepted as a purely logical axiom. In lectures from the Summer term 1920, he concluded that “the aim of reducing set theory, an ...
... In about 1920, Hilbert came to reject Russell’s logicist solution to the consistency problem for arithmetic, mainly for the reason that the axiom of reducibility cannot be accepted as a purely logical axiom. In lectures from the Summer term 1920, he concluded that “the aim of reducing set theory, an ...
Propositional Logic
... A logical language can be used in different ways. For instance, a language can be used as a deduction system (or proof system); that is, to construct proofs or refutations. This use of a logical language is called proof theory. In this case, a set of facts called axioms and a set of deduction rules ...
... A logical language can be used in different ways. For instance, a language can be used as a deduction system (or proof system); that is, to construct proofs or refutations. This use of a logical language is called proof theory. In this case, a set of facts called axioms and a set of deduction rules ...
Advanced Logic —
... P ROOF. Suppose IND is true, but for a reductio, suppose that LNP is not. Then there is some subset B ⊆ N such that: (1) B is not empty; and (2) B has no least element. Let A = N\B. Clearly 0 ∈ / B (for then 0 would be the least element), so 0 ∈ A. Moreover, since B has no least element, this just m ...
... P ROOF. Suppose IND is true, but for a reductio, suppose that LNP is not. Then there is some subset B ⊆ N such that: (1) B is not empty; and (2) B has no least element. Let A = N\B. Clearly 0 ∈ / B (for then 0 would be the least element), so 0 ∈ A. Moreover, since B has no least element, this just m ...
lecture notes in logic - UCLA Department of Mathematics
... As we read these formulas in English (unabbreviating the formal symbols), the first two of them say exactly the same thing: that we can add some number to v2 and get 0—which is true exactly when v2 is a name of 0. The third formula says the same thing about whatever number v5 names, which need not b ...
... As we read these formulas in English (unabbreviating the formal symbols), the first two of them say exactly the same thing: that we can add some number to v2 and get 0—which is true exactly when v2 is a name of 0. The third formula says the same thing about whatever number v5 names, which need not b ...
PDF
... Choose r = 0, prove 02≤0 ∧ 0<(0+1)2 using standard arithmetic – Step case: assume ∃rn r2≤n ∧ n<(rn+1)2 and prove ∃r r 2≤n+1 ∧ n+1<(r+1)2 ...
... Choose r = 0, prove 02≤0 ∧ 0<(0+1)2 using standard arithmetic – Step case: assume ∃rn r2≤n ∧ n<(rn+1)2 and prove ∃r r 2≤n+1 ∧ n+1<(r+1)2 ...
On the structure of honest elementary degrees - FAU Math
... Q sum and bounded product, that is, respectively f (~x, y) = i
... Q sum and bounded product, that is, respectively f (~x, y) = i
logic for computer science - Institute for Computing and Information
... Gottlob Frege, a German mathematician working in relative obscurity. Frege aimed to derive all of mathematics from logical principles, in other words pure reason, together with some self-evident truths about sets. (Such as 'sets are identical if they have the same members' or 'every property determi ...
... Gottlob Frege, a German mathematician working in relative obscurity. Frege aimed to derive all of mathematics from logical principles, in other words pure reason, together with some self-evident truths about sets. (Such as 'sets are identical if they have the same members' or 'every property determi ...