COMPLETELY RANK-NONINCREASING LINEAR MAPS Don
... A, (Aeλ , fλ ) → tr(A), where tr denotes the normalized trace on M2 . This follows from the fact that the above assertion is equivalent to the rank-two matrix 12 I2 being the weak*-limit in the dual space of M2 (which is M2 ) of the net rank-one elements eλ ⊗ fλ . To construct the counterexample, le ...
... A, (Aeλ , fλ ) → tr(A), where tr denotes the normalized trace on M2 . This follows from the fact that the above assertion is equivalent to the rank-two matrix 12 I2 being the weak*-limit in the dual space of M2 (which is M2 ) of the net rank-one elements eλ ⊗ fλ . To construct the counterexample, le ...
Selected Exercises 1. Let M and N be R
... 20. Let R be a Noetherian commutative ring and Q an injective R-module. Fix an ideal I ⊆ R and set ΓI (Q) := {x ∈ Q | I n x = 0, for some n ≥ 0}. Show that ΓI (Q) is an injective R-module. 21. Let A and B be R-modules. Set I := annR (A) and J := annR (B). Show that I + J ⊆ annR (ExtnR (A, B)), for a ...
... 20. Let R be a Noetherian commutative ring and Q an injective R-module. Fix an ideal I ⊆ R and set ΓI (Q) := {x ∈ Q | I n x = 0, for some n ≥ 0}. Show that ΓI (Q) is an injective R-module. 21. Let A and B be R-modules. Set I := annR (A) and J := annR (B). Show that I + J ⊆ annR (ExtnR (A, B)), for a ...
Holt Algebra 1 11-EXT
... radical sign. It indicate what root you are taking. This is the index (plural, indices) of the radical. When a radical is written without an index, the index is understood to be 2. Only positive integers greater than or equal to 2 may be indices of radicals. Holt Algebra 1 ...
... radical sign. It indicate what root you are taking. This is the index (plural, indices) of the radical. When a radical is written without an index, the index is understood to be 2. Only positive integers greater than or equal to 2 may be indices of radicals. Holt Algebra 1 ...
Solutions Sheet 7
... Solution: (a) If X were affine, it would be isomorphic to Spec OX (X). We claim that this is not the case. Similarly to the example of P1k in the lecture, we compute the ring of global sections OX (X) = OX (U1 ) ∩ OX (U2 ), where the intersection is as subrings of OX (U12 ) = k[X1 , X1−1 ]. This yie ...
... Solution: (a) If X were affine, it would be isomorphic to Spec OX (X). We claim that this is not the case. Similarly to the example of P1k in the lecture, we compute the ring of global sections OX (X) = OX (U1 ) ∩ OX (U2 ), where the intersection is as subrings of OX (U12 ) = k[X1 , X1−1 ]. This yie ...
ORTHOPOSETS WITH QUANTIFIERS 1. Introduction
... P is a structured atlas as described in the theorem. By Corollary 2.2, then all operations ∃t are quantifiers. It remains to prove that ∃s ∃t = ∃s∧t for all s and t in T . We may proceed as in the proof of Theorem ??(c) if the right-hand side in the identity (ii) does not depend of the choice of s. ...
... P is a structured atlas as described in the theorem. By Corollary 2.2, then all operations ∃t are quantifiers. It remains to prove that ∃s ∃t = ∃s∧t for all s and t in T . We may proceed as in the proof of Theorem ??(c) if the right-hand side in the identity (ii) does not depend of the choice of s. ...
FREE-BY-FREE GROUPS OVER POLYNOMIALLY GROWING
... σ(tj )(xi ) = xi for any i = 1, · · · , n − 1 and j = 1, · · · , n − 1 whereas σ(tj )(xn ) = xn xj for j = 1, · · · , n − 1. A particularity of σ(Fn−1 ) is to have linear growth: Definition 3. An automorphism α of a group G with finite generating S has polynomial growth if and only if there is a pol ...
... σ(tj )(xi ) = xi for any i = 1, · · · , n − 1 and j = 1, · · · , n − 1 whereas σ(tj )(xn ) = xn xj for j = 1, · · · , n − 1. A particularity of σ(Fn−1 ) is to have linear growth: Definition 3. An automorphism α of a group G with finite generating S has polynomial growth if and only if there is a pol ...
3. Localization.
... (2) Is it true that if A has no nilpotent elements different from zero then Ap has no nilpotent elements different from zero for all prime ideals p of A? 7. Let M be a finitely generated A module, and let S be a multiplicatively closed subset of M . Show that S −1 M = 0 if and only if there is an el ...
... (2) Is it true that if A has no nilpotent elements different from zero then Ap has no nilpotent elements different from zero for all prime ideals p of A? 7. Let M be a finitely generated A module, and let S be a multiplicatively closed subset of M . Show that S −1 M = 0 if and only if there is an el ...
TERNARY BOOLEAN ALGEBRA 1. Introduction. The
... I t is necessary only to consider the automorphism of K t h a t transforms p into q. This transforms the operations of B{p) into the corresponding ones of B{q). 6. Realizations of the ternary algebra. We have pointed out t h a t the function {aC\b)\J (br\c)KJ {cC\a) in Boolean algebra satisfies the ...
... I t is necessary only to consider the automorphism of K t h a t transforms p into q. This transforms the operations of B{p) into the corresponding ones of B{q). 6. Realizations of the ternary algebra. We have pointed out t h a t the function {aC\b)\J (br\c)KJ {cC\a) in Boolean algebra satisfies the ...
Affine Hecke Algebra Modules i
... algebras in the references provided. We prove a basis theorem for these algebras and use the basis theorem to show that the cyclotomic Hecke algebras are symmetric algebras. The main references for this part of the talk is [GJ11, 5.1-5.2]. Auxilliary useful references include [AK94, BM97, MM98] and ...
... algebras in the references provided. We prove a basis theorem for these algebras and use the basis theorem to show that the cyclotomic Hecke algebras are symmetric algebras. The main references for this part of the talk is [GJ11, 5.1-5.2]. Auxilliary useful references include [AK94, BM97, MM98] and ...
2-5 Complex Numbers and Roots 2-5 Complex Numbers
... quadratic functions? • Find the zeros of the related equation by completing the square and taking the square root of each side. Simplify the radical of the negative number by replacing with the imaginary unit i. Holt McDougal Algebra 2 ...
... quadratic functions? • Find the zeros of the related equation by completing the square and taking the square root of each side. Simplify the radical of the negative number by replacing with the imaginary unit i. Holt McDougal Algebra 2 ...
the farrell-jones isomorphism conjecture for finite covolume
... Let Γ be a discrete group, let ZΓ denote its integral group ring, and let Ki (ZΓ) be the algebraic K-theory groups of the ring ZΓ, where i ∈ Z. It has been conjectured that these K-groups may be computed from the corresponding K-groups of certain subgroups of Γ. More precisely, the Farrell-Jones Iso ...
... Let Γ be a discrete group, let ZΓ denote its integral group ring, and let Ki (ZΓ) be the algebraic K-theory groups of the ring ZΓ, where i ∈ Z. It has been conjectured that these K-groups may be computed from the corresponding K-groups of certain subgroups of Γ. More precisely, the Farrell-Jones Iso ...
The Type of the Classifying Space of a Topological Group for the
... Recall from the introduction the G-CW -complex E(G, F ). In particular, notice that we do not work with the stronger condition that E(G, F )H is contractible but only weakly contractible. If G is discrete, then each fixed point set E(G, F )H has the homotopy type of a CW -complex and is contractible ...
... Recall from the introduction the G-CW -complex E(G, F ). In particular, notice that we do not work with the stronger condition that E(G, F )H is contractible but only weakly contractible. If G is discrete, then each fixed point set E(G, F )H has the homotopy type of a CW -complex and is contractible ...
8.2 CONJUGATES AND DIVISION OF COMPLEX NUMBERS
... zz 5 sa 1 bidsa 2 bid 5 a 2 1 abi 2 abi 2 b2i 2 5 a 2 1 b2. The second and third properties follow directly from the first. Finally, the fourth property follows the definition of complex conjugate. That is, (z ) 5 (a 1 bi) 5 a 2 bi 5 a 1 bi 5 z . ...
... zz 5 sa 1 bidsa 2 bid 5 a 2 1 abi 2 abi 2 b2i 2 5 a 2 1 b2. The second and third properties follow directly from the first. Finally, the fourth property follows the definition of complex conjugate. That is, (z ) 5 (a 1 bi) 5 a 2 bi 5 a 1 bi 5 z . ...
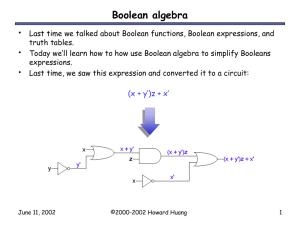
Boolean Algebra
... A sum of products (SOP) expression is characterized by: – There are only OR (sum) operations at the “outermost” level. – Each term in the sum must be a product of literals. For example: f(x,y,z) = y’ + x’yz’ + xz ...
... A sum of products (SOP) expression is characterized by: – There are only OR (sum) operations at the “outermost” level. – Each term in the sum must be a product of literals. For example: f(x,y,z) = y’ + x’yz’ + xz ...
Introduction, modular theory and classification theory
... The conventional definition of a von Neumann algebra is that it is a unital *subalgebra of L(H) which satisfies the equivalent conditions above. The equivalence with our earlier ‘simplest definition’ is a consequence of the double commutant theorem and the fact that any element of a von Neumann alge ...
... The conventional definition of a von Neumann algebra is that it is a unital *subalgebra of L(H) which satisfies the equivalent conditions above. The equivalence with our earlier ‘simplest definition’ is a consequence of the double commutant theorem and the fact that any element of a von Neumann alge ...
Real Composition Algebras by Steven Clanton
... binary (rank 2) quadratic forms. In particular, Gauss proved that any positive definite binary quadratic form can be linearly transformed into the two-squares formula w12 + w22 = (u21 + u22 ) (v12 + v22 ). This shows not only the existence of an algebra for every form but also an isomorphism to the ...
... binary (rank 2) quadratic forms. In particular, Gauss proved that any positive definite binary quadratic form can be linearly transformed into the two-squares formula w12 + w22 = (u21 + u22 ) (v12 + v22 ). This shows not only the existence of an algebra for every form but also an isomorphism to the ...
An introduction to random walks on groups
... Example 1.4. Let Γ = (V, E) be a locally finite graph. In other words, V (vertices) is a set, E ⊂ V × V (edges) is a symmetric relation (that is, for any (x, y) in E, one has (y, x) ∈ E) and, for any x in V , the set of y in V such that (x, y) ∈ E is finite. For x in V and n in N, we let Bn (x) be ...
... Example 1.4. Let Γ = (V, E) be a locally finite graph. In other words, V (vertices) is a set, E ⊂ V × V (edges) is a symmetric relation (that is, for any (x, y) in E, one has (y, x) ∈ E) and, for any x in V , the set of y in V such that (x, y) ∈ E is finite. For x in V and n in N, we let Bn (x) be ...