MTH55_Lec-13_sec_3-3a_3Var_Lin_Sys
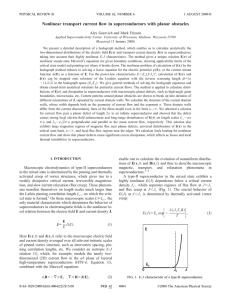
... Substituting into either equation (4) or (5) we find that x = 1 Now we have x = 1 and y = 2. To find the value for z, we use any of the three original equations and substitute to find the third number z. Let’s use eqn (1) x+y+z=6 and substitute our 1 + 2 + z = 6 two numbers in it: z = 3. Chabo ...
... Substituting into either equation (4) or (5) we find that x = 1 Now we have x = 1 and y = 2. To find the value for z, we use any of the three original equations and substitute to find the third number z. Let’s use eqn (1) x+y+z=6 and substitute our 1 + 2 + z = 6 two numbers in it: z = 3. Chabo ...
Flux emergence: flares and coronal mass ejections driven by dynamo action
... can be observed, for example, by certain spectral lines of Hα, CaII H and K, which have much lower intensity because of the decreased density. The bottom of the chromosphere is defined by the radial temperature minimum of the Sun. This is mostly set to 500 km above the optical limb, depending on the ...
... can be observed, for example, by certain spectral lines of Hα, CaII H and K, which have much lower intensity because of the decreased density. The bottom of the chromosphere is defined by the radial temperature minimum of the Sun. This is mostly set to 500 km above the optical limb, depending on the ...
Review Assessment: q01
... information given, each particle could have any velocity greater than or equal to 0 but less than the speed of light. We have no way of knowing what the velocity of either particle is. ...
... information given, each particle could have any velocity greater than or equal to 0 but less than the speed of light. We have no way of knowing what the velocity of either particle is. ...
Document
... Whether a field is seen as “electric” or “magnetic” depends on the motion of the reference frame relative to the sources of the field. Copyright © 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley. ...
... Whether a field is seen as “electric” or “magnetic” depends on the motion of the reference frame relative to the sources of the field. Copyright © 2008 Pearson Education, Inc., publishing as Pearson Addison-Wesley. ...
ABSTRACT Title of Dissertation: SYNTHESIS
... the ME effect have been proposed. In one such device configuration, the desired effect is electric field tuning of giant magnetoresistance or tunnel magnetoresistance through control of exchange bias via the ME effect. We have investigated the feasibility of such a device using exchange-biased Co/Pt ...
... the ME effect have been proposed. In one such device configuration, the desired effect is electric field tuning of giant magnetoresistance or tunnel magnetoresistance through control of exchange bias via the ME effect. We have investigated the feasibility of such a device using exchange-biased Co/Pt ...
Two New Theories for the Current Charge Relativity and the Electric
... (3) the Biot-Savart law, and (4) the magnetic force law between two current elements. This paper proposes new theories that integrate work from these topics to provide an explanation for the magnetic force using the concept of electric force. A. Filamentary Current The current is filamentary when it ...
... (3) the Biot-Savart law, and (4) the magnetic force law between two current elements. This paper proposes new theories that integrate work from these topics to provide an explanation for the magnetic force using the concept of electric force. A. Filamentary Current The current is filamentary when it ...
electrostatic potential and capacitance
... FIGURE 2.1 A test charge q (> 0) is R to P, we apply an external force Fext just enough to moved from the point R to the counter the repulsive electric force FE (i.e, Fext= –FE). point P against the repulsive force on it by the charge Q (> 0) This means there is no net force on or acceleration of pl ...
... FIGURE 2.1 A test charge q (> 0) is R to P, we apply an external force Fext just enough to moved from the point R to the counter the repulsive electric force FE (i.e, Fext= –FE). point P against the repulsive force on it by the charge Q (> 0) This means there is no net force on or acceleration of pl ...
No Slide Title
... experience a force when close to other electrically charged matter. Two types, Positive and Negative Like charges repel, unlike ones attract. Positive charge comes from having more protons than electrons; Negative charge comes from having more electrons than protons. Charge is quantized. That is, wh ...
... experience a force when close to other electrically charged matter. Two types, Positive and Negative Like charges repel, unlike ones attract. Positive charge comes from having more protons than electrons; Negative charge comes from having more electrons than protons. Charge is quantized. That is, wh ...