Characteristics of quasi-static potential structures observed in the
... and with electrostatic structures extending over this altitude range. In their study no distinction was made between divergent and convergent electric field structures in the return current region and primary current region, respectively. Janhunen et al. (1999) used Polar data to investigate whether ...
... and with electrostatic structures extending over this altitude range. In their study no distinction was made between divergent and convergent electric field structures in the return current region and primary current region, respectively. Janhunen et al. (1999) used Polar data to investigate whether ...
Capacitors
... The electric field due to the plates is directed to the right and it polarizes the dielectric The net effect on the dielectric is an induced surface charge that results in an induced electric field If the dielectric were replaced with a conductor, the net field between the plates would be ...
... The electric field due to the plates is directed to the right and it polarizes the dielectric The net effect on the dielectric is an induced surface charge that results in an induced electric field If the dielectric were replaced with a conductor, the net field between the plates would be ...
4 Measurements
... both the electric and magnetic fields must be calculated or measured. In practice, however, this may prove very difficult to accomplish. ...
... both the electric and magnetic fields must be calculated or measured. In practice, however, this may prove very difficult to accomplish. ...
Faraday`s Law and Induction lecture notes
... Answer: (c). Specifically: c, d = e, b, a. The magnitude of the emf is proportional to the rate of change of the magnetic flux. This is proportional to the rate of change of the magnetic field – i.e. the change in the slope of the graph. The magnitude of the slope is largest at c. Points d and e are ...
... Answer: (c). Specifically: c, d = e, b, a. The magnitude of the emf is proportional to the rate of change of the magnetic flux. This is proportional to the rate of change of the magnetic field – i.e. the change in the slope of the graph. The magnitude of the slope is largest at c. Points d and e are ...
Magnetic Fields
... A rectangular coil of dimensions 5.40 cm by 8.50 cm consists of 25 turns of wire. The coil carries a current of 15 mA. A uniform magnetic field of magnitude 0.350 T is applied parallel to the plane of the loop. What are the magnitudes of the magnetic moment of the coil and the torque acting on the l ...
... A rectangular coil of dimensions 5.40 cm by 8.50 cm consists of 25 turns of wire. The coil carries a current of 15 mA. A uniform magnetic field of magnitude 0.350 T is applied parallel to the plane of the loop. What are the magnitudes of the magnetic moment of the coil and the torque acting on the l ...
Chapter 16 Solutions
... directed either radially toward or radially away from the point charge. From rule 2: The magnitude of the field due to the point charge only depends on the distance from the point charge. Thus the density of the field lines must be the same at any location around the point charge for a given distanc ...
... directed either radially toward or radially away from the point charge. From rule 2: The magnitude of the field due to the point charge only depends on the distance from the point charge. Thus the density of the field lines must be the same at any location around the point charge for a given distanc ...
RECOMMENDATION ITU-R BS.1698 - Evaluating
... both the electric and magnetic fields must be calculated or measured. In practice, however, this may prove very difficult to accomplish. ...
... both the electric and magnetic fields must be calculated or measured. In practice, however, this may prove very difficult to accomplish. ...
Document
... electric field always produces a magnetic field. This interaction of electric and magnetic forces gives rise to a condition in space known as an electromagnetic field. The characteristics of an electromagnetic field are expressed mathematically by Maxwell's equation. Vector A directed line segment. ...
... electric field always produces a magnetic field. This interaction of electric and magnetic forces gives rise to a condition in space known as an electromagnetic field. The characteristics of an electromagnetic field are expressed mathematically by Maxwell's equation. Vector A directed line segment. ...
Active Materials Embedded in Photonic Crystals and Coupled to Electromagnetic Radiation
... can be done in either order兲. The cycle is repeated for each time step until all electric, magnetic, and polarization fields have decayed to negligible magnitudes. In this work, stimulated emission at frequency 1 is desired, which requires a population inversion between the two intermediate levels ...
... can be done in either order兲. The cycle is repeated for each time step until all electric, magnetic, and polarization fields have decayed to negligible magnitudes. In this work, stimulated emission at frequency 1 is desired, which requires a population inversion between the two intermediate levels ...
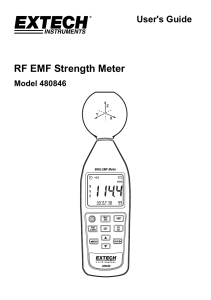
RF EMF Strength Meter
... This meter is a broadband device for monitoring high-frequency radiation in the range of 10MHz to 8GHz. The non-directional electric field and high sensitivity also allow measurements of electric field strength in TEM cells and absorber rooms. The unit of measurement and the measurement types are ex ...
... This meter is a broadband device for monitoring high-frequency radiation in the range of 10MHz to 8GHz. The non-directional electric field and high sensitivity also allow measurements of electric field strength in TEM cells and absorber rooms. The unit of measurement and the measurement types are ex ...
Anglická verze kvartonovky
... "accompany" each body as it moves through space, but did not realize that along with rotating outer layers of the body structure as well as the globe rotates gravitational field. It is obvious that this rotating gravitational environment in which electromagnetic waves are spreading, showed Michelson ...
... "accompany" each body as it moves through space, but did not realize that along with rotating outer layers of the body structure as well as the globe rotates gravitational field. It is obvious that this rotating gravitational environment in which electromagnetic waves are spreading, showed Michelson ...
32.2. The Induced Electric
... general. It holds for rods and wires of arbitrary shape moving through arbitrary magnetic fields. Equation (32.5) relates the induced emf to the rate at which the enclosed magnetic flux changes. In the system shown in Figure 32.1 the enclosed flux changes due to the motion of the rod. The enclosed m ...
... general. It holds for rods and wires of arbitrary shape moving through arbitrary magnetic fields. Equation (32.5) relates the induced emf to the rate at which the enclosed magnetic flux changes. In the system shown in Figure 32.1 the enclosed flux changes due to the motion of the rod. The enclosed m ...
Downloadable Full Text
... of these potential problems in electrostatics, as well as in other areas of physical, engineering and technological applications. According to the basic approach towards solving electrostatic problems, methods can be roughly divided into either finite element methods (FEM), boundary element methods ...
... of these potential problems in electrostatics, as well as in other areas of physical, engineering and technological applications. According to the basic approach towards solving electrostatic problems, methods can be roughly divided into either finite element methods (FEM), boundary element methods ...
Gravitation
... - Biswas3 shows that a Lorentz covariant modification of the Newtonian potential contributes about 43 arc-secs/century. A second-rank symmetric tensor is introduced into special relativity – as a potential rather than a metric. 11. The Pioneer effect ...
... - Biswas3 shows that a Lorentz covariant modification of the Newtonian potential contributes about 43 arc-secs/century. A second-rank symmetric tensor is introduced into special relativity – as a potential rather than a metric. 11. The Pioneer effect ...
Field (physics)
In physics, a field is a physical quantity that has a value for each point in space and time. For example, on a weather map, the surface wind velocity is described by assigning a vector to each point on a map. Each vector represents the speed and direction of the movement of air at that point. As another example, an electric field can be thought of as a ""condition in space"" emanating from an electric charge and extending throughout the whole of space. When a test electric charge is placed in this electric field, the particle accelerates due to a force. Physicists have found the notion of a field to be of such practical utility for the analysis of forces that they have come to think of a force as due to a field.In the modern framework of the quantum theory of fields, even without referring to a test particle, a field occupies space, contains energy, and its presence eliminates a true vacuum. This lead physicists to consider electromagnetic fields to be a physical entity, making the field concept a supporting paradigm of the edifice of modern physics. ""The fact that the electromagnetic field can possess momentum and energy makes it very real... a particle makes a field, and a field acts on another particle, and the field has such familiar properties as energy content and momentum, just as particles can have"". In practice, the strength of most fields has been found to diminish with distance to the point of being undetectable. For instance the strength of many relevant classical fields, such as the gravitational field in Newton's theory of gravity or the electrostatic field in classical electromagnetism, is inversely proportional to the square of the distance from the source (i.e. they follow the Gauss's law). One consequence is that the Earth's gravitational field quickly becomes undetectable on cosmic scales.A field can be classified as a scalar field, a vector field, a spinor field or a tensor field according to whether the represented physical quantity is a scalar, a vector, a spinor or a tensor, respectively. A field has a unique tensorial character in every point where it is defined: i.e. a field cannot be a scalar field somewhere and a vector field somewhere else. For example, the Newtonian gravitational field is a vector field: specifying its value at a point in spacetime requires three numbers, the components of the gravitational field vector at that point. Moreover, within each category (scalar, vector, tensor), a field can be either a classical field or a quantum field, depending on whether it is characterized by numbers or quantum operators respectively. In fact in this theory an equivalent representation of field is a field particle, namely a boson.