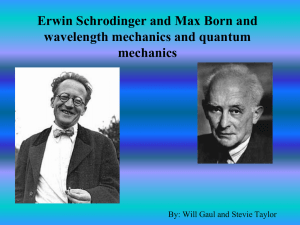String Theory
... Newton. Newton invented Calculus so that problems involving moving objects could be solved. ...
... Newton. Newton invented Calculus so that problems involving moving objects could be solved. ...
Field and gauge theories
... Infinities arise in calculated quantities Infinities in QED are results of closed loops of virtual particles – must integrate over all possible values of momentum around loop and momentum is not uniquely defined (off-the-shell) Closely related to failures of classical EM, like infinite selfene ...
... Infinities arise in calculated quantities Infinities in QED are results of closed loops of virtual particles – must integrate over all possible values of momentum around loop and momentum is not uniquely defined (off-the-shell) Closely related to failures of classical EM, like infinite selfene ...
3quarksdaily: More Is Different
... the time. They wondered where, in this crazy space, lay the innocent realm in which they dwelled before the quantum interrupted. In answer, Niels Bohr came up with his famous correspondence principle. The classical laws we are familiar with might not be applicable to microscopic realms, he said, but ...
... the time. They wondered where, in this crazy space, lay the innocent realm in which they dwelled before the quantum interrupted. In answer, Niels Bohr came up with his famous correspondence principle. The classical laws we are familiar with might not be applicable to microscopic realms, he said, but ...
A Brief Introduction into Quantum Gravity and Quantum Cosmology
... no external time present; spacetime has disappeared! ...
... no external time present; spacetime has disappeared! ...
Quantum mechanic and Particle physics
... about physical laws. Boltzmann had shown how thermodynamic equilibrium is established by means of a statistical equilibrium, and if such an approach is applied to the equilibrium between matter and radiation, one finds that the continuous loss of energy into radiation can be prevented by assuming th ...
... about physical laws. Boltzmann had shown how thermodynamic equilibrium is established by means of a statistical equilibrium, and if such an approach is applied to the equilibrium between matter and radiation, one finds that the continuous loss of energy into radiation can be prevented by assuming th ...
LanZ_0112_eps(1).
... This thesis explores Feynman’s idea of quantum simulations by using ultracold quantum gases. In the first part of the thesis we develop a general method applicable to atoms or molecules or even nanoparticles, to decelerate a hot fast gas beam to zero velocity by using an optical cavity. This deceler ...
... This thesis explores Feynman’s idea of quantum simulations by using ultracold quantum gases. In the first part of the thesis we develop a general method applicable to atoms or molecules or even nanoparticles, to decelerate a hot fast gas beam to zero velocity by using an optical cavity. This deceler ...
Erwin Schrodinger an Max Born and wavelength
... Erwin Schrodinger and wavelength mechanics • In 1926 he determined that a particle or an atom would vibrate in circles with activity • The atom contained, “Waves of Chance” • When an electron passed through the nucleus these waves would ripple back and forth • They would ripple in a straight line w ...
... Erwin Schrodinger and wavelength mechanics • In 1926 he determined that a particle or an atom would vibrate in circles with activity • The atom contained, “Waves of Chance” • When an electron passed through the nucleus these waves would ripple back and forth • They would ripple in a straight line w ...
The Hilbert Space of Quantum Gravity Is Locally Finite
... map HR ⊗ HR̄ → HR ⊗ HR̄ represents an approximation. In particular, our ability to divide space into two sets of degrees of freedom doesn’t imply that we can continue to subdivide it into many small regions simultaneously.) Such a decomposition is familiar in the case of quantum field theories on a ...
... map HR ⊗ HR̄ → HR ⊗ HR̄ represents an approximation. In particular, our ability to divide space into two sets of degrees of freedom doesn’t imply that we can continue to subdivide it into many small regions simultaneously.) Such a decomposition is familiar in the case of quantum field theories on a ...
Quantum Field Theory
... high energies requires the use of special relativity. In some circumstances - think about elementary particle physics e.g. - one gets confronted with phenomena which simultaneously occur at high energies and small scales. The framework which unifies special relativity with quantum mechanics is relat ...
... high energies requires the use of special relativity. In some circumstances - think about elementary particle physics e.g. - one gets confronted with phenomena which simultaneously occur at high energies and small scales. The framework which unifies special relativity with quantum mechanics is relat ...
4.Operator representations and double phase space
... For a symplectic transformation there is only one branch of y(x) and the semiclassical form is exact. In general there may be caustics, where the Lagrangian surface projects singularly onto the y=0 plane. (the identity plane) Turning on a Hamiltonian for a small time: No caustics ! ...
... For a symplectic transformation there is only one branch of y(x) and the semiclassical form is exact. In general there may be caustics, where the Lagrangian surface projects singularly onto the y=0 plane. (the identity plane) Turning on a Hamiltonian for a small time: No caustics ! ...
IV3416201624
... Such systems are clocks. A clock stands, ideally, in the same simple relation to the universal time coordinate t as a point particle stands to the universal space coordinate x. We may generally define an ideal clock as a physical system which has a dynamical variable which behaves under time transla ...
... Such systems are clocks. A clock stands, ideally, in the same simple relation to the universal time coordinate t as a point particle stands to the universal space coordinate x. We may generally define an ideal clock as a physical system which has a dynamical variable which behaves under time transla ...
Chapter 2 Quantum statistical mechanics from classical
... in certain models in 1+1 dimensions. Such models are called integrable, and as a consequence some quantities can be computed exactly by using techniques such as the Bethe ...
... in certain models in 1+1 dimensions. Such models are called integrable, and as a consequence some quantities can be computed exactly by using techniques such as the Bethe ...
周正威
... two-body terms. With the interactions restricted to nearest neighbors, The ground state can be obtained through one of the following methods: i) by extracting it from the solution of the DMRG method; ii) by considering any product state, and by using the present scheme to simulate an evolution in im ...
... two-body terms. With the interactions restricted to nearest neighbors, The ground state can be obtained through one of the following methods: i) by extracting it from the solution of the DMRG method; ii) by considering any product state, and by using the present scheme to simulate an evolution in im ...