ppt
... “All Cretans are liars.” Equivalently: “This statement is false.” Russell’s types can help with the set paradox, but not with this one. ...
... “All Cretans are liars.” Equivalently: “This statement is false.” Russell’s types can help with the set paradox, but not with this one. ...
Löwenheim-Skolem theorems and Choice principles
... with the sentences ci 6= cj for i 6= j. Since ℵ0 ≤ µ and there are only a finite number of symbols in φ, the new signature has cardinality µ. Also, since µ ≤ κ, M contains µ many different elements and hence can be turned into a model of T by using these as the interpretations of the constant symbo ...
... with the sentences ci 6= cj for i 6= j. Since ℵ0 ≤ µ and there are only a finite number of symbols in φ, the new signature has cardinality µ. Also, since µ ≤ κ, M contains µ many different elements and hence can be turned into a model of T by using these as the interpretations of the constant symbo ...
CHAPTER 1 INTRODUCTION 1 Mathematical Paradoxes
... a suitable set of axioms. If we do so, we obtain an axiomatic set theory without such antinomies. The problem arises what set of axioms should be chosen in order to obtain a sufficiently rich theory of sets. The first such axiomatic set theory was invented by Zermello in 1908. In chapter .. we shal ...
... a suitable set of axioms. If we do so, we obtain an axiomatic set theory without such antinomies. The problem arises what set of axioms should be chosen in order to obtain a sufficiently rich theory of sets. The first such axiomatic set theory was invented by Zermello in 1908. In chapter .. we shal ...
Title PI name/institution
... Integrated Enzyme-Logic systems for Monitoring and Treating Autonomously Injured Soldiers Joseph Wang (UCSD) and Evgeny Katz (Clarkson University) Project Objectives: To develop next-generation ‘sense and treat’ autonomous devices for enhancing the survival rate among A) injured soldiers in the batt ...
... Integrated Enzyme-Logic systems for Monitoring and Treating Autonomously Injured Soldiers Joseph Wang (UCSD) and Evgeny Katz (Clarkson University) Project Objectives: To develop next-generation ‘sense and treat’ autonomous devices for enhancing the survival rate among A) injured soldiers in the batt ...
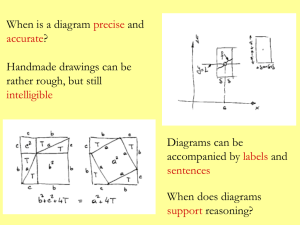
Diagrams in logic and mathematics - CFCUL
... 1. ontological statements are in general much more problematic than the difficulties they are intended to find solution to the infinite debate about the ontological nature of mathematical objects shows that it is very problematic to settle ontological questions once and for all Balaguer (1998) 2. ev ...
... 1. ontological statements are in general much more problematic than the difficulties they are intended to find solution to the infinite debate about the ontological nature of mathematical objects shows that it is very problematic to settle ontological questions once and for all Balaguer (1998) 2. ev ...
characterization of prime numbers by
... Thus, x → y differs from x → y in that x → y does not always take the k designated value n − 1 when x < y and if x = y then x → y = n − 1 only when x ∈ {0, 1, n − 1}. Logic Kn is defined in analogy with Ln , and Kn is the set of all matrix functions from Kn . To prove the theorems the following two ...
... Thus, x → y differs from x → y in that x → y does not always take the k designated value n − 1 when x < y and if x = y then x → y = n − 1 only when x ∈ {0, 1, n − 1}. Logic Kn is defined in analogy with Ln , and Kn is the set of all matrix functions from Kn . To prove the theorems the following two ...
Stephen Cook and Phuong Nguyen. Logical foundations of proof
... reverse mathematics one would look for the weakest theory of bounded arithmetic in which the most important theorems that are relevant to computer science can be proved. The book includes several such examples from the recent literature in this area, such as feasible proofs of the Cayley–Hamilton Th ...
... reverse mathematics one would look for the weakest theory of bounded arithmetic in which the most important theorems that are relevant to computer science can be proved. The book includes several such examples from the recent literature in this area, such as feasible proofs of the Cayley–Hamilton Th ...
Second order logic or set theory?
... complete sentences are categorical. • Ajtai, Solovay: Consistently, there are complete sentences that are non-‐categorical. • Again, ``φ is complete” is not Π2-‐definable. ...
... complete sentences are categorical. • Ajtai, Solovay: Consistently, there are complete sentences that are non-‐categorical. • Again, ``φ is complete” is not Π2-‐definable. ...
PHIL012 Class Notes
... • “a=b” means that “a” and “b” are names that refer to the same objects, which can denote numbers or sets. • “a=b” also means that whatever claims are made of a must also be true of b (and vice versa) if “a=b” is true. ...
... • “a=b” means that “a” and “b” are names that refer to the same objects, which can denote numbers or sets. • “a=b” also means that whatever claims are made of a must also be true of b (and vice versa) if “a=b” is true. ...
Bound and Free Variables Theorems and Proofs
... using a random process, that puts each edge in with probability 1/2. ...
... using a random process, that puts each edge in with probability 1/2. ...
Gödel`s First Incompleteness Theorem
... “This sentence is false!” Kurt Gödel had a genius for turning such philosophical paradoxes into formal mathematics. In a recursively enumerable axiomatisation, T , all sentences — statements and proofs of statements — can, in principle, be listed systematically, although this enumeration will never ...
... “This sentence is false!” Kurt Gödel had a genius for turning such philosophical paradoxes into formal mathematics. In a recursively enumerable axiomatisation, T , all sentences — statements and proofs of statements — can, in principle, be listed systematically, although this enumeration will never ...
course notes - Theory and Logic Group
... Theorem 1.5 (Löwenheim-Skolem). Every satisfiable set of sentences has a countable model. Proof. Let Γ be a set of sentences. First, if Γ is satisfiable then ClpΓq is consistent, for suppose ClpΓq would not be consistent, then there would be a proof of Γ0 Ñ K for Γ0 Γ, so Γ0 would not be satisfia ...
... Theorem 1.5 (Löwenheim-Skolem). Every satisfiable set of sentences has a countable model. Proof. Let Γ be a set of sentences. First, if Γ is satisfiable then ClpΓq is consistent, for suppose ClpΓq would not be consistent, then there would be a proof of Γ0 Ñ K for Γ0 Γ, so Γ0 would not be satisfia ...
FOR HIGHER-ORDER RELEVANT LOGIC
... and theories. Thus far, γ has at most been proved, in [2], for first-order relevant logics. (Related methods are applied, in [1], to yield a new proof of elementary logic, the classical adaptation of the γ-techniques as refined in [3] having been carried out by Dunn.) It is time to move up; at the h ...
... and theories. Thus far, γ has at most been proved, in [2], for first-order relevant logics. (Related methods are applied, in [1], to yield a new proof of elementary logic, the classical adaptation of the γ-techniques as refined in [3] having been carried out by Dunn.) It is time to move up; at the h ...
comments on the logic of constructible falsity (strong negation)
... be proven in the same way) completeness of essentially the logic described here relative to essentially this model theory. His proof proceeds by showing that a predicate logic incorporating both − and ¬ and relating them by the rule that −A implies ¬A is a conservative extension of intuitionistic lo ...
... be proven in the same way) completeness of essentially the logic described here relative to essentially this model theory. His proof proceeds by showing that a predicate logic incorporating both − and ¬ and relating them by the rule that −A implies ¬A is a conservative extension of intuitionistic lo ...
Proof Theory - Andrew.cmu.edu
... free in any hypothesis. For intuitionistic logic, one also needs the rule ex falso sequitur quodlibet, which allows one to conclude Γ ⇒ ϕ from Γ ⇒ ⊥, where ⊥ represents falsity. One can then define negation, ¬ϕ, as ϕ → ⊥. For classical logic, one adds reductio ad absurdum, or proof by contradiction, ...
... free in any hypothesis. For intuitionistic logic, one also needs the rule ex falso sequitur quodlibet, which allows one to conclude Γ ⇒ ϕ from Γ ⇒ ⊥, where ⊥ represents falsity. One can then define negation, ¬ϕ, as ϕ → ⊥. For classical logic, one adds reductio ad absurdum, or proof by contradiction, ...
Chapter Nine - Queen of the South
... consistent but which elude deductive proof in axiomatic systems. Given his own terms of reference within a specified context like Principia Mathematica, Gödel's fundamental concepts of selfinsufficiency and of other-dependence are quite valid logically. The formal method of his monumental Proof may ...
... consistent but which elude deductive proof in axiomatic systems. Given his own terms of reference within a specified context like Principia Mathematica, Gödel's fundamental concepts of selfinsufficiency and of other-dependence are quite valid logically. The formal method of his monumental Proof may ...
Set theory, by Thomas Jech, Academic Press, New York, 1978, xii +
... consistency of formal axiomatic systems, always require some elementary use of mathematical logic for their rigorous explication. The first consistency result of mathematical significance was GödeFs proof, around 1938, that the GCH is consistent with ZFC. Much later, around 1963, Cohen showed that t ...
... consistency of formal axiomatic systems, always require some elementary use of mathematical logic for their rigorous explication. The first consistency result of mathematical significance was GödeFs proof, around 1938, that the GCH is consistent with ZFC. Much later, around 1963, Cohen showed that t ...