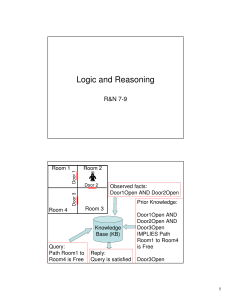
Forward chaining
... Resolution Systems and Deduction Shallow and Causal Reasoning Resolution and First-Order Predicate Logic Forward and Backward Chaining Other Methods of Inference Metaknowledge ...
... Resolution Systems and Deduction Shallow and Causal Reasoning Resolution and First-Order Predicate Logic Forward and Backward Chaining Other Methods of Inference Metaknowledge ...
Chapter 2.6 Notes: Prove Statements about Segments and Angles
... • A proof is a logical argument that shows a satement is true. Two-Column Proofs: • A two-column proof has numbered statements and corresponding reasons that show an argument in a logical order. • In a two-column proof, each statement in the lefthand column is either given information or the result ...
... • A proof is a logical argument that shows a satement is true. Two-Column Proofs: • A two-column proof has numbered statements and corresponding reasons that show an argument in a logical order. • In a two-column proof, each statement in the lefthand column is either given information or the result ...
1 TRUTH AND MEANING Ian Rumfitt C.E.M. Joad`s catchphrase—`It
... In defining truth as it applies to beliefs, Ramsey takes as understood the notion of a belief’s being a belief that P. Similarly, in explicating truth as it applies to statements, Strawson takes as understood the notion of a statement’s saying that things are thusand-so. That is, bot ...
... In defining truth as it applies to beliefs, Ramsey takes as understood the notion of a belief’s being a belief that P. Similarly, in explicating truth as it applies to statements, Strawson takes as understood the notion of a statement’s saying that things are thusand-so. That is, bot ...
Document
... In all of these cases P(k) can be either true or false. For example, in the last case, P(1) is false because the sum is 1 and 1 , 10, but P(4) is true because 1 + 2 + 3 + 4 = 10. Exercise 1: For each statement in the list above, determine (without proof) the natural numbers for which the statement i ...
... In all of these cases P(k) can be either true or false. For example, in the last case, P(1) is false because the sum is 1 and 1 , 10, but P(4) is true because 1 + 2 + 3 + 4 = 10. Exercise 1: For each statement in the list above, determine (without proof) the natural numbers for which the statement i ...
Operators
... Operators Operators are symbols such as + (addition), - (subtraction), and * (multiplication). Operators do something with values. $foo = 25; $foo – 15; // $foo and 15 are the operands, - is the operator ...
... Operators Operators are symbols such as + (addition), - (subtraction), and * (multiplication). Operators do something with values. $foo = 25; $foo – 15; // $foo and 15 are the operands, - is the operator ...
A game semantics for proof search: Preliminary results - LIX
... productive and has allowed the development of a number of logic programming languages based on logics other than first-order classical logic. The following observation appears, however, to be an interesting challenge to this approach to logic programming. Consider a simple “logic engine” that will a ...
... productive and has allowed the development of a number of logic programming languages based on logics other than first-order classical logic. The following observation appears, however, to be an interesting challenge to this approach to logic programming. Consider a simple “logic engine” that will a ...
Intuitionistic Logic
... A proof of A∧B is simply a pair of proofs a and b of A and B. For convenience we introduce a a notation for the pairing of constructions, and for the inverses (projections); (a, b) denotes the pairing of a and b, and (c)0 ,(c)1 , are the first and second projection of c. Now, the proof of a disjunc ...
... A proof of A∧B is simply a pair of proofs a and b of A and B. For convenience we introduce a a notation for the pairing of constructions, and for the inverses (projections); (a, b) denotes the pairing of a and b, and (c)0 ,(c)1 , are the first and second projection of c. Now, the proof of a disjunc ...
What Is Answer Set Programming?
... (a closed path that passes through each vertex of the graph exactly once). The ASP program below should be combined with definitions of the predicates vertex and edge, as in the previous example. It uses the predicate in to express that an edge belongs to the path; we assume that 0 is one of the ver ...
... (a closed path that passes through each vertex of the graph exactly once). The ASP program below should be combined with definitions of the predicates vertex and edge, as in the previous example. It uses the predicate in to express that an edge belongs to the path; we assume that 0 is one of the ver ...
MMConceptualComputationalRemainder
... the maximum of the set of common divisors of the two numbers, and a set of numbers has only one maximum. I have shown my students this proof many times, but they almost never reproduce it on an examination. ...
... the maximum of the set of common divisors of the two numbers, and a set of numbers has only one maximum. I have shown my students this proof many times, but they almost never reproduce it on an examination. ...
ctl
... A CTL formula is built from three things: 1. Atomic propositions - These are the variables 2. Boolean connectives - AND, OR, NOT, etc. 3. Temporal operators - Express something about paths in the computational tree A temporal operator has two parts: 1. A path quantifier - A (for all paths) or E (the ...
... A CTL formula is built from three things: 1. Atomic propositions - These are the variables 2. Boolean connectives - AND, OR, NOT, etc. 3. Temporal operators - Express something about paths in the computational tree A temporal operator has two parts: 1. A path quantifier - A (for all paths) or E (the ...