Unit 1C - Rational Numbers
... Coordinate grid (plane): A plane formed by the intersection of a horizontal line called the x-axis and a vertical line called the y-axis. Ordered pair: A pair of numbers that can be used to locate a point on a coordinate plane. Origin: The point where the x-axis and y-axis intersect on the coo ...
... Coordinate grid (plane): A plane formed by the intersection of a horizontal line called the x-axis and a vertical line called the y-axis. Ordered pair: A pair of numbers that can be used to locate a point on a coordinate plane. Origin: The point where the x-axis and y-axis intersect on the coo ...
1.1 Segments, Rays, and Distance
... ◦ The geometry that we are most familiar with is called Euclidian Geometry named after the mathematician Euclid who realized/discovered/defined 5 (some argue 6) basic undeniable rules in which set the foundation for all other rules in geometry. Without Euclid’s 5 absolute truths (axioms) we would no ...
... ◦ The geometry that we are most familiar with is called Euclidian Geometry named after the mathematician Euclid who realized/discovered/defined 5 (some argue 6) basic undeniable rules in which set the foundation for all other rules in geometry. Without Euclid’s 5 absolute truths (axioms) we would no ...
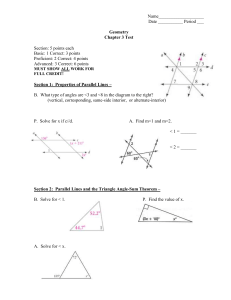
Test 3 Review
... Most of the examples below are odd-numbered exercises in the Geometry textbook, so you can check the answers for them in the back of the book. (Selected Answers start at page 831.) Work the examples on a separate sheet of paper. Students should be able to: ...
... Most of the examples below are odd-numbered exercises in the Geometry textbook, so you can check the answers for them in the back of the book. (Selected Answers start at page 831.) Work the examples on a separate sheet of paper. Students should be able to: ...
Title: Finding the midpoint of a number line segment
... Essential Question(s) How do I (HDI) name and label geometric figures? HDI determine the dimensions of an object? HDI calculate straight and diagonal distances formulaically? Objective(s) Students will be able to (SWBAT) correlate antiblobbiness with geometry. SWBAT use appropriate notatio ...
... Essential Question(s) How do I (HDI) name and label geometric figures? HDI determine the dimensions of an object? HDI calculate straight and diagonal distances formulaically? Objective(s) Students will be able to (SWBAT) correlate antiblobbiness with geometry. SWBAT use appropriate notatio ...
Medium Term Planning Year 4 Theme 7 Theme Title: Solve
... familiar with different orientations of lines of symmetry; and recognise line symmetry in a variety of diagrams including where the line of symmetry does not dissect the reflected shape. ...
... familiar with different orientations of lines of symmetry; and recognise line symmetry in a variety of diagrams including where the line of symmetry does not dissect the reflected shape. ...
Geometry - Piscataway High School
... o Use tracing paper investigations with ruler and protractor – should we find a specific activity? Define congruence through rigid transformations on the coordinate plane and validate using distance formula and midpoint formula Define compositions of transformations to map congruent figures onto one ...
... o Use tracing paper investigations with ruler and protractor – should we find a specific activity? Define congruence through rigid transformations on the coordinate plane and validate using distance formula and midpoint formula Define compositions of transformations to map congruent figures onto one ...
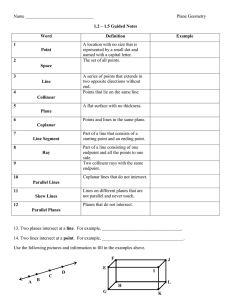
Name Plane Geometry 1.2 – 1.5 Guided Notes Word Definition
... named with a capital letter. The set of all points. ...
... named with a capital letter. The set of all points. ...
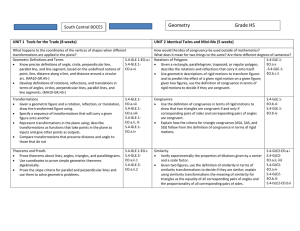
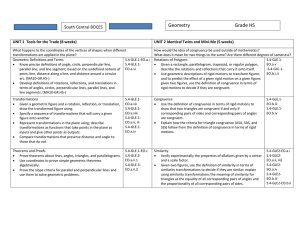
Geometry Scope and Sequence
... What happens to the coordinates of the vertices of shapes when different transformations are applied in the plane? Geometric Definitions and Terms S.4-GLE.1-EO.a.i S.4-GLE.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notion ...
... What happens to the coordinates of the vertices of shapes when different transformations are applied in the plane? Geometric Definitions and Terms S.4-GLE.1-EO.a.i S.4-GLE.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notion ...
1 2. SCALARS, VECTORS, TENSORS, AND DYADS This section is
... coordinates can be obtained by everywhere replacing the derivative !iV j with the covariant derivative DiV j , defined by Equation (2.45). In analogy with the discussion preceding Equation (2.32), covariant differentiation is often expressed in the shorthand notation Di A jk ! A..;ijk . Meisner, Tho ...
... coordinates can be obtained by everywhere replacing the derivative !iV j with the covariant derivative DiV j , defined by Equation (2.45). In analogy with the discussion preceding Equation (2.32), covariant differentiation is often expressed in the shorthand notation Di A jk ! A..;ijk . Meisner, Tho ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.