Semester Exam Review - Chagrin Falls Schools
... III. outside the triangle a. I only b. II only c. I or II only d. I, II, or II ____ 62. Where can the bisectors of the angles of an obtuse triangle intersect? I. inside the triangle II. on the triangle III. outside the triangle a. I only b. III only c. I or III only ____ 63. In ACE, G is the centro ...
... III. outside the triangle a. I only b. II only c. I or II only d. I, II, or II ____ 62. Where can the bisectors of the angles of an obtuse triangle intersect? I. inside the triangle II. on the triangle III. outside the triangle a. I only b. III only c. I or III only ____ 63. In ACE, G is the centro ...
MATH - Amazon Web Services
... The six parts of a two-column proof are listed in order: Statement: a full written statement of the theorem. Figure: a lettered figure drawn to illustrate the given conditions of the statement. Given: the given conditions of the statement expressed in terms of the letter and numerals used in the fig ...
... The six parts of a two-column proof are listed in order: Statement: a full written statement of the theorem. Figure: a lettered figure drawn to illustrate the given conditions of the statement. Given: the given conditions of the statement expressed in terms of the letter and numerals used in the fig ...
Section 7A
... graph provided. Which point is an x-intercept? Which point is a y-intercept? For the other three points, give the quadrant they lie in. ...
... graph provided. Which point is an x-intercept? Which point is a y-intercept? For the other three points, give the quadrant they lie in. ...
Finish the Semester
... While we are on the topic of angles let's briefly discuss a topic that comes up in some exercises – the number of degrees in a triangle. We have discussed the three-sided polygon before in terms of its perimeter, but we have not discussed any other properties of this figure. Since there are three s ...
... While we are on the topic of angles let's briefly discuss a topic that comes up in some exercises – the number of degrees in a triangle. We have discussed the three-sided polygon before in terms of its perimeter, but we have not discussed any other properties of this figure. Since there are three s ...
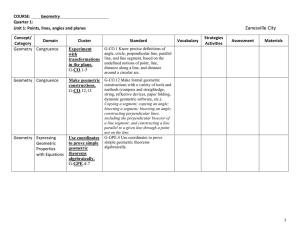
Geometry Year at a Glance Unit 1: Congruence, Proofs, and
... Unit 4: Connecting Algebra and Geometry through Coordinates Unit overview: (Narrative description of unit purpose) Building on their work with the Pythagorean theorem in 8th grade to find distances, students analyze geometric relationships in the context of a rectangular coordinate system, including ...
... Unit 4: Connecting Algebra and Geometry through Coordinates Unit overview: (Narrative description of unit purpose) Building on their work with the Pythagorean theorem in 8th grade to find distances, students analyze geometric relationships in the context of a rectangular coordinate system, including ...
TN Geometry Traditional Pacing Guide 2017-18
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. Represent transformations in the plane using transparencies and geometry software; describe transf ...
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. Represent transformations in the plane using transparencies and geometry software; describe transf ...
Cartesian coordinate system
A Cartesian coordinate system is a coordinate system that specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis of the system, and the point where they meet is its origin, usually at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, n Cartesian coordinates (an element of real n-space) specify the point in an n-dimensional Euclidean space for any dimension n. These coordinates are equal, up to sign, to distances from the point to n mutually perpendicular hyperplanes.The invention of Cartesian coordinates in the 17th century by René Descartes (Latinized name: Cartesius) revolutionized mathematics by providing the first systematic link between Euclidean geometry and algebra. Using the Cartesian coordinate system, geometric shapes (such as curves) can be described by Cartesian equations: algebraic equations involving the coordinates of the points lying on the shape. For example, a circle of radius 2 in a plane may be described as the set of all points whose coordinates x and y satisfy the equation x2 + y2 = 4.Cartesian coordinates are the foundation of analytic geometry, and provide enlightening geometric interpretations for many other branches of mathematics, such as linear algebra, complex analysis, differential geometry, multivariate calculus, group theory and more. A familiar example is the concept of the graph of a function. Cartesian coordinates are also essential tools for most applied disciplines that deal with geometry, including astronomy, physics, engineering and many more. They are the most common coordinate system used in computer graphics, computer-aided geometric design and other geometry-related data processing.