B + Tree
... Indexed sequential access method (ISAM) • Data entries vs index entries – Both belong to index file – Data entries:
– Index entries:
...
... Indexed sequential access method (ISAM) • Data entries vs index entries – Both belong to index file – Data entries:
slides
... Open Addressing • Basic idea (details in Section 12.4): – To insert: if slot is full, try another slot, …, until an open slot is found (probing) – To search, follow same sequence of probes as would be used when inserting the element • If reach element with correct key, return it • If reach a NULL p ...
... Open Addressing • Basic idea (details in Section 12.4): – To insert: if slot is full, try another slot, …, until an open slot is found (probing) – To search, follow same sequence of probes as would be used when inserting the element • If reach element with correct key, return it • If reach a NULL p ...
binary search tree
... Child and Parent Every node except the root has one parent A node can have zero or more children Leaves: nodes with no children Also called external nodes Internal node: having one or more children Siblings: nodes having the same parent ...
... Child and Parent Every node except the root has one parent A node can have zero or more children Leaves: nodes with no children Also called external nodes Internal node: having one or more children Siblings: nodes having the same parent ...
Operations on Trees and Priority Queues
... the heap property (“for each subtree, the key of the root is greater or equal than all the value in the subtree”.) Your implementation should support the following methods: 1. bool isEmpty() 2. void insert(int value): inserts a value into the queue. Hints: Insertion should keep, as far as possible, ...
... the heap property (“for each subtree, the key of the root is greater or equal than all the value in the subtree”.) Your implementation should support the following methods: 1. bool isEmpty() 2. void insert(int value): inserts a value into the queue. Hints: Insertion should keep, as far as possible, ...
Data Structures and Algorithms Binary Search Tree
... The left sub-tree of a node has key less than or equal to its parent node's key. The right sub-tree of a node has key greater than or equal to its parent node's key. Thus, a binary search tree BST divides all its sub-trees into two segments; left sub-tree and right sub-tree and can be defined as − l ...
... The left sub-tree of a node has key less than or equal to its parent node's key. The right sub-tree of a node has key greater than or equal to its parent node's key. Thus, a binary search tree BST divides all its sub-trees into two segments; left sub-tree and right sub-tree and can be defined as − l ...
Search/Insert Properties of BSTs
... Best case (balanced): about lg N nodes between root and each external node/leaf Worst case (unbalanced): about N nodes between root and each external node/leaf With random data: – trees are likely to be well-balanced on average ...
... Best case (balanced): about lg N nodes between root and each external node/leaf Worst case (unbalanced): about N nodes between root and each external node/leaf With random data: – trees are likely to be well-balanced on average ...
Cache-Oblivious Priority Queue and Graph Algorithm
... External Memory Data Structures • General-purpose data structures – Space: linear or near-linear (very important) – Query: logarithmic in B or 2 for any query (very important) – Update: logarithmic in B or 2 (important) • In some sense, more useful than I/O-algorithms – Structure stored in disk mos ...
... External Memory Data Structures • General-purpose data structures – Space: linear or near-linear (very important) – Query: logarithmic in B or 2 for any query (very important) – Update: logarithmic in B or 2 (important) • In some sense, more useful than I/O-algorithms – Structure stored in disk mos ...
Presentation on Implementing Binary Trees
... • Check if the new node belongs left or right from the runner, then.... ...
... • Check if the new node belongs left or right from the runner, then.... ...
Slides 3 - USC Upstate: Faculty
... Disadvantages of BST The shape of the tree depends on the order of insertions, and it can be degenerated. When inserting or searching for an element, the key of each visited node has to be compared with the key of the element to be inserted/found. Keys may be long and the run time may increase ...
... Disadvantages of BST The shape of the tree depends on the order of insertions, and it can be degenerated. When inserting or searching for an element, the key of each visited node has to be compared with the key of the element to be inserted/found. Keys may be long and the run time may increase ...
of a tree
... Children of a node ordered (List of children). Children of a node unordered (Set/Bag of children). Item in each node is less than items in child nodes. Item at each node is smaller that all items in its left subtree and greater than all items in its right subtree. ...
... Children of a node ordered (List of children). Children of a node unordered (Set/Bag of children). Item in each node is less than items in child nodes. Item at each node is smaller that all items in its left subtree and greater than all items in its right subtree. ...
Exam Review 2 - City University of New York
... Binary Search Trees (BSTs) • Binary search trees are a good implementation of data types such as sets, bags, and dictionaries. • Searching for an item is generally quick since you move from the root to the item, without looking at many other items. • Adding and deleting items is also quick. • But a ...
... Binary Search Trees (BSTs) • Binary search trees are a good implementation of data types such as sets, bags, and dictionaries. • Searching for an item is generally quick since you move from the root to the item, without looking at many other items. • Adding and deleting items is also quick. • But a ...
Document
... Finite collection of nodes Each node has exactly one parent, but for the root node Each node may have up to n children A leaf node has no children An interior node is a node that is not a leaf ...
... Finite collection of nodes Each node has exactly one parent, but for the root node Each node may have up to n children A leaf node has no children An interior node is a node that is not a leaf ...
tree
... Non-linear structures Other organizations are possible, (e.g., file organization on disk is a tree) c: \drivers ...
... Non-linear structures Other organizations are possible, (e.g., file organization on disk is a tree) c: \drivers ...
Data Structures and Search Algorithms
... Traverse: Pre-order v. Post-order v. Inorder Node, edge, sibling/parent/child, leaf ...
... Traverse: Pre-order v. Post-order v. Inorder Node, edge, sibling/parent/child, leaf ...
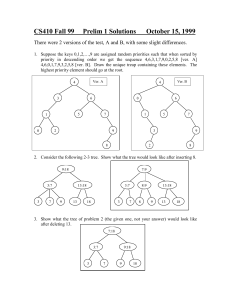
Prelim 1 solutions - Cornell Computer Science
... All operations should take worst-case time O(log n). You may use any of the data structures we have discussed in class without saying how they work, but describe in detail any modifications you need to do to achieve the desired time bounds, and describe in detail your implementation of count. Use an ...
... All operations should take worst-case time O(log n). You may use any of the data structures we have discussed in class without saying how they work, but describe in detail any modifications you need to do to achieve the desired time bounds, and describe in detail your implementation of count. Use an ...
B-tree
In computer science, a B-tree is a tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree is a generalization of a binary search tree in that a node can have more than two children (Comer 1979, p. 123). Unlike self-balancing binary search trees, the B-tree is optimized for systems that read and write large blocks of data. B-trees are a good example of a data structure for external memory. It is commonly used in databases and filesystems.