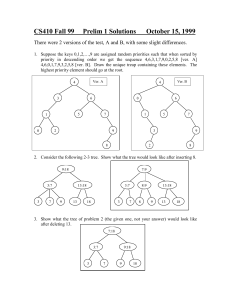
Prelim 1 solutions - Cornell Computer Science
... structures we have discussed in class without saying how they work, but describe in detail any modifications you need to do to achieve the desired time bounds, and describe in detail your implementation of count. Use any balanced tree scheme for dictionaries such as 2-3 trees or red-black trees. Aug ...
... structures we have discussed in class without saying how they work, but describe in detail any modifications you need to do to achieve the desired time bounds, and describe in detail your implementation of count. Use any balanced tree scheme for dictionaries such as 2-3 trees or red-black trees. Aug ...
Concurrent R
... ◦ The key for each internal node is the minimum bounding rectangle of its child nodes ...
... ◦ The key for each internal node is the minimum bounding rectangle of its child nodes ...
Trees and Binary Search Trees Dynamic data structures Tree: Tree:
... Depth of a node: length of path from root to that node. Height of a node: length of longest path from node to a leaf. - height of tree = height of root, depth of deepest leaf - leaves have height 0 ...
... Depth of a node: length of path from root to that node. Height of a node: length of longest path from node to a leaf. - height of tree = height of root, depth of deepest leaf - leaves have height 0 ...
Data structure
... Each link in the root node refers to a child A node with no children is called a leaf node ...
... Each link in the root node refers to a child A node with no children is called a leaf node ...
Lect14
... give you O(log n) behavior. It is not a tree. In this data structure we keep multiple parallel sorted linked lists with each list being longer than the one before it. The trick is keeping track of the right elements. ...
... give you O(log n) behavior. It is not a tree. In this data structure we keep multiple parallel sorted linked lists with each list being longer than the one before it. The trick is keeping track of the right elements. ...
CSE 114 – Computer Science I Lecture 1
... • To squeeze performance out of our program – more efficient memory management – faster for certain problems ...
... • To squeeze performance out of our program – more efficient memory management – faster for certain problems ...
Data Structures and Algorithms Binary Search Tree
... The left sub-tree of a node has key less than or equal to its parent node's key. The right sub-tree of a node has key greater than or equal to its parent node's key. Thus, a binary search tree BST divides all its sub-trees into two segments; left sub-tree and right sub-tree and can be defined as − l ...
... The left sub-tree of a node has key less than or equal to its parent node's key. The right sub-tree of a node has key greater than or equal to its parent node's key. Thus, a binary search tree BST divides all its sub-trees into two segments; left sub-tree and right sub-tree and can be defined as − l ...
Session 1
... Tree Creation, Searching a value in a binary search tree, Depth First Traversal of the tree, Tree Traversals - Preorder traversal of the tree, Post-order traversal of the tree, In order Traversal, Functions to find Predecessor, Successor, Parent, Brother, To delete a node from the tree,Expression tr ...
... Tree Creation, Searching a value in a binary search tree, Depth First Traversal of the tree, Tree Traversals - Preorder traversal of the tree, Post-order traversal of the tree, In order Traversal, Functions to find Predecessor, Successor, Parent, Brother, To delete a node from the tree,Expression tr ...
Midterm (with solution)
... 4. AVL method. A heap is a complete binary tree (it is completely filled with the exeption of the bottom level) since it adds elements in a breath first manner (top down and from left to right for each level). 5. Inorder traversal ...
... 4. AVL method. A heap is a complete binary tree (it is completely filled with the exeption of the bottom level) since it adds elements in a breath first manner (top down and from left to right for each level). 5. Inorder traversal ...
CS 104 Introduction to Computer Science and Graphics Problems
... Application: Binary Search Tree, Heap ...
... Application: Binary Search Tree, Heap ...
Trees Types and Operations
... ◦ replace the key of that node with the minimum element at the right subtree (or the maximum element at the left subtree) ◦ delete the minimum element Has either no child or only right child because if it has a left child, that left child would be smaller and would have been chosen. So invoke case ...
... ◦ replace the key of that node with the minimum element at the right subtree (or the maximum element at the left subtree) ◦ delete the minimum element Has either no child or only right child because if it has a left child, that left child would be smaller and would have been chosen. So invoke case ...
Binary search tree
In computer science, binary search trees (BST), sometimes called ordered or sorted binary trees, are a particular type of containers: data structures that store ""items"" (such as numbers, names and etc.) in memory. They allow fast lookup, addition and removal of items, and can be used to implement either dynamic sets of items, or lookup tables that allow finding an item by its key (e.g., finding the phone number of a person by name).Binary search trees keep their keys in sorted order, so that lookup and other operations can use the principle of binary search: when looking for a key in a tree (or a place to insert a new key), they traverse the tree from root to leaf, making comparisons to keys stored in the nodes of the tree and deciding, based on the comparison, to continue searching in the left or right subtrees. On average, this means that each comparison allows the operations to skip about half of the tree, so that each lookup, insertion or deletion takes time proportional to the logarithm of the number of items stored in the tree. This is much better than the linear time required to find items by key in an (unsorted) array, but slower than the corresponding operations on hash tables.They are a special case of the more general B-tree with order equal to two.























