Exact, Efficient, and Complete Arrangement Computation for Cubic
... Suppose we can compute gcds in a UFD R. Then we can also compute gcd(f, g) for non-zero f, g ∈ R[x]: Because of Corollary 2, gcd(f, g) is, up to a constant factor, the gcd of f, g regarded as elements of Q(R)[x], and we can compute that with the Euclidean Algorithm. Using Corollary 4, the error in t ...
... Suppose we can compute gcds in a UFD R. Then we can also compute gcd(f, g) for non-zero f, g ∈ R[x]: Because of Corollary 2, gcd(f, g) is, up to a constant factor, the gcd of f, g regarded as elements of Q(R)[x], and we can compute that with the Euclidean Algorithm. Using Corollary 4, the error in t ...
END
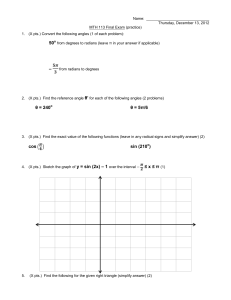
... (a) Prove that P1 , P2 , P3 and P4 lie on a circle if and only if t1 t2 t3 t4 = 1 . (b) State the relationship between the hyperbola and the circle through the points P1, P3 and P4 if t12 t3 t4 = 1 . (c) Given a point P, with parameter t and t2 1, on the hyperbola. Show that there exist two circle ...
... (a) Prove that P1 , P2 , P3 and P4 lie on a circle if and only if t1 t2 t3 t4 = 1 . (b) State the relationship between the hyperbola and the circle through the points P1, P3 and P4 if t12 t3 t4 = 1 . (c) Given a point P, with parameter t and t2 1, on the hyperbola. Show that there exist two circle ...
Formulae Connecting Segments of the Same Line Pure Geometry
... thus the point has gone from A to B. The fundamental formulae then are (1) AB = – BA; (2) AB = OB – OA. In the above discussion the lengths have been taken on a line. But this is not necessary; the lengths might have been taken on any curve. It is generally convenient to use an abridged form of the ...
... thus the point has gone from A to B. The fundamental formulae then are (1) AB = – BA; (2) AB = OB – OA. In the above discussion the lengths have been taken on a line. But this is not necessary; the lengths might have been taken on any curve. It is generally convenient to use an abridged form of the ...
![Elliptic curves with Q( E[3]) = Q( ζ3)](http://s1.studyres.com/store/data/012817289_1-48789e28be1e09d726c6f57e08e36eee-300x300.png)
ExamView - chapter 7 review.tst
... 5. Two lines that have the same slope are said to be _________________________ . 6. Perpendicular lines have slopes that are _________________________ . ...
... 5. Two lines that have the same slope are said to be _________________________ . 6. Perpendicular lines have slopes that are _________________________ . ...
Geometry classwork1 September 16
... One can formally define an operation of addition on the set of all vectors (in the space of vectors). For any two vectors, and , such an operation results in a third vector, , such that three following rules hold, ...
... One can formally define an operation of addition on the set of all vectors (in the space of vectors). For any two vectors, and , such an operation results in a third vector, , such that three following rules hold, ...
Closed sets and the Zariski topology
... Theorem 2.4 (Hilbert Basissatz). Let k be an arbitrary field (not necessarily infinite). Then the polynomial ring k[x1 , . . . , xn ] is Noetherian. A more general version of this is Theorem 2.5. If R is Noetherian, then so is the polynomial ring R[x] (in one variable). We will prove theorem 2.4. Fo ...
... Theorem 2.4 (Hilbert Basissatz). Let k be an arbitrary field (not necessarily infinite). Then the polynomial ring k[x1 , . . . , xn ] is Noetherian. A more general version of this is Theorem 2.5. If R is Noetherian, then so is the polynomial ring R[x] (in one variable). We will prove theorem 2.4. Fo ...
Lesson 7.6 Properties of Systems of Linear Equations Exercises
... The second line does not intersect this line, so it has the same slope but different y-intercept. Let the y-intercept be –3; the slope is 2. Use the slope-intercept form to write the equation of the second line as: y = 2x – 3 A linear system is: –2x + y = 1 y = 2x – 3 c) One equation of a linear sys ...
... The second line does not intersect this line, so it has the same slope but different y-intercept. Let the y-intercept be –3; the slope is 2. Use the slope-intercept form to write the equation of the second line as: y = 2x – 3 A linear system is: –2x + y = 1 y = 2x – 3 c) One equation of a linear sys ...
Homogeneous coordinates
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry, as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix.If the homogeneous coordinates of a point are multiplied by a non-zero scalar then the resulting coordinates represent the same point. Since homogeneous coordinates are also given to points at infinity, the number of coordinates required to allow this extension is one more than the dimension of the projective space being considered. For example, two homogeneous coordinates are required to specify a point on the projective line and three homogeneous coordinates are required to specify a point in the projective plane.