Solving Systems of Linear Equations
... Multiply one or both equations by factors that will prove opposites coefficients for one of the variables, if needed. Add the equations to eliminate one equation and one variable. Solve the linear equation obtained in step 3. Do one of the following: A. Substitute the value obtained in step 4 into e ...
... Multiply one or both equations by factors that will prove opposites coefficients for one of the variables, if needed. Add the equations to eliminate one equation and one variable. Solve the linear equation obtained in step 3. Do one of the following: A. Substitute the value obtained in step 4 into e ...
Problem Set #2
... Note: Use RREF on your calculator, unless you need to do by hand, as in #1 and #3. 1. Solve the system of linear equations by row reducing the augmented matrix by hand to convert it to row-reduced echelon form. Show all steps and label each elementary row operation. 3x 7 y z 11 2x y 2z ...
... Note: Use RREF on your calculator, unless you need to do by hand, as in #1 and #3. 1. Solve the system of linear equations by row reducing the augmented matrix by hand to convert it to row-reduced echelon form. Show all steps and label each elementary row operation. 3x 7 y z 11 2x y 2z ...
Solving Systems Using Word Problems Objectives
... mile head start on Frank. If Melissa ran at an average rate of 5 miles per hour and Frank ran at an average rate of 8 miles per hour, how long would it take for Frank to catch up with Melissa? ...
... mile head start on Frank. If Melissa ran at an average rate of 5 miles per hour and Frank ran at an average rate of 8 miles per hour, how long would it take for Frank to catch up with Melissa? ...
Solving Systems of Linear Equations By Elimination
... of the variables (x or y) using addition and or subtraction. ...
... of the variables (x or y) using addition and or subtraction. ...
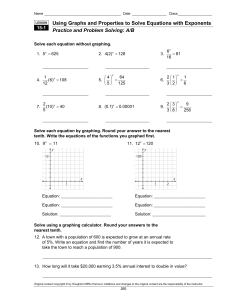
3.4 Solving Equations with Variables on Both Sides
... • Some equations have variables on both sides • To solve these equations, you can first collect the variable terms on one side of the equation • Collecting the variable terms on the side with the greater variable coefficient will result in a positive coefficient ...
... • Some equations have variables on both sides • To solve these equations, you can first collect the variable terms on one side of the equation • Collecting the variable terms on the side with the greater variable coefficient will result in a positive coefficient ...
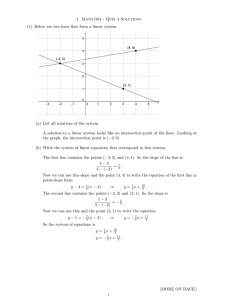
Solving Systems of Equations by Graphing PowerPoint
... These two lines intersect at the point (2, 1) which is the solution to the system of equations. (consistent and independent) ...
... These two lines intersect at the point (2, 1) which is the solution to the system of equations. (consistent and independent) ...
Use for “null set” (no solutions)
... Section 2.2 Using the Principles Together Clearing Fractions and Decimals from an equation If given a choice, most of us would rather work a problem in whole numbers rather than fractions or decimals. We’re going to look at a little gimmick that will “clear the factions” from an equations. We’re goi ...
... Section 2.2 Using the Principles Together Clearing Fractions and Decimals from an equation If given a choice, most of us would rather work a problem in whole numbers rather than fractions or decimals. We’re going to look at a little gimmick that will “clear the factions” from an equations. We’re goi ...
Solving Systems of Linear Equations By Elimination
... How is solving by elimination similar to solving by substitution? ...
... How is solving by elimination similar to solving by substitution? ...