Is there a preferred canonical quantum gauge?
... from (10). The non-commutativity of Po and /i’ in (10) can also be physically understood as being due to the fact that a measurement of /3’ results in the angular acceleration )~‘ of the cylinder which produces an electric field which changes p,, which has the meaning ofthe kinetic angular momentum ...
... from (10). The non-commutativity of Po and /i’ in (10) can also be physically understood as being due to the fact that a measurement of /3’ results in the angular acceleration )~‘ of the cylinder which produces an electric field which changes p,, which has the meaning ofthe kinetic angular momentum ...
Charged Particle in an Electromagnetic Field
... ~ B) ~ for any choice of f = f (t, ~x). Because all the physics in classical define the same (E, ~ and B, ~ we declare that all potentials related by such electrodynamics is determined by E gauge transformations are physically equivalent in the classical setting. In the quantum setting, we must like ...
... ~ B) ~ for any choice of f = f (t, ~x). Because all the physics in classical define the same (E, ~ and B, ~ we declare that all potentials related by such electrodynamics is determined by E gauge transformations are physically equivalent in the classical setting. In the quantum setting, we must like ...
***** 1
... The physical Hamiltonian H(ph) depends, in general, on a chosen parametrization and gauge. In particular, for the ADM parametrization and the condition N = 1 the left-hand side of this equation coincides with the lefthand side of the Wheeler − DeWitt equation. In Quantum Geometrodynamics in extended ...
... The physical Hamiltonian H(ph) depends, in general, on a chosen parametrization and gauge. In particular, for the ADM parametrization and the condition N = 1 the left-hand side of this equation coincides with the lefthand side of the Wheeler − DeWitt equation. In Quantum Geometrodynamics in extended ...
kavic_Poster0216
... made great progress in understanding QCD, however, analytic understanding has not come as far. ...
... made great progress in understanding QCD, however, analytic understanding has not come as far. ...
Quantum simulators of lattice gauge theories
... II. The simulated models have to be of some relevance for applications and/or our understanding of challenges of condensed matter, high energy physics, or more generally quantum many body physics. III. The simulated models should be computationally very hard for classical computers (meaning= no effi ...
... II. The simulated models have to be of some relevance for applications and/or our understanding of challenges of condensed matter, high energy physics, or more generally quantum many body physics. III. The simulated models should be computationally very hard for classical computers (meaning= no effi ...
SU(3) Multiplets & Gauge Invariance
... the lowest dimensional representation of SU(3) – the set of 3-dimensional matrices – must act on, and their eigenvalues describe, a set of real physical states,with quantum numbers: ...
... the lowest dimensional representation of SU(3) – the set of 3-dimensional matrices – must act on, and their eigenvalues describe, a set of real physical states,with quantum numbers: ...
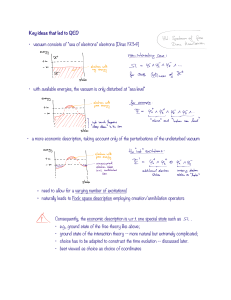
Key ideas that led to QED vacuum consists of "sea of electrons
... Many symbolic manipulations have to conducted on the integrant such as: • normal ordering due to the infinitely many charges in the Dirac sea; • mass renormalization due to the ultraviolet/infrared divergence of the photon field; • charge renormalization, again due to the infinitely many charges in ...
... Many symbolic manipulations have to conducted on the integrant such as: • normal ordering due to the infinitely many charges in the Dirac sea; • mass renormalization due to the ultraviolet/infrared divergence of the photon field; • charge renormalization, again due to the infinitely many charges in ...
YANG-MILLS THEORY 1. Introduction In 1954, Yang and Mills
... In the previous section, the transition from global to local symmetries was introduced in a rather ad hoc fashion. The covariant derivative and the gauge field were not motivated in any depth. In this section, we will see that these objects follow from geometrical arguments. Once again we try to fin ...
... In the previous section, the transition from global to local symmetries was introduced in a rather ad hoc fashion. The covariant derivative and the gauge field were not motivated in any depth. In this section, we will see that these objects follow from geometrical arguments. Once again we try to fin ...
Document
... Perturbative expansion of S-matrix contains Time ordered product of interaction Hamiltonian. To find transition amplitude one need to find ...
... Perturbative expansion of S-matrix contains Time ordered product of interaction Hamiltonian. To find transition amplitude one need to find ...
Syllabus : Advanced Quantum Mechanics (Prof
... The emphasis is on the application of field theoretic concepts and methods to understand and be able to calculate such diverse effects as: spontaneous emission and decay rates, scattering crosssections (including their polarization dependence), relativistic corrections, the Lamb shift and Casimir- a ...
... The emphasis is on the application of field theoretic concepts and methods to understand and be able to calculate such diverse effects as: spontaneous emission and decay rates, scattering crosssections (including their polarization dependence), relativistic corrections, the Lamb shift and Casimir- a ...
Dia 1
... But what about higher loop diagrams? It would be elegant if you could use 6, 7, or more dimensions. But this did not work ! A last, desparate attempt: Take 4 dimensions and use Dimensional renormalization ! ...
... But what about higher loop diagrams? It would be elegant if you could use 6, 7, or more dimensions. But this did not work ! A last, desparate attempt: Take 4 dimensions and use Dimensional renormalization ! ...
A first view on the mathematical structure of the standard
... the symmetry group is non-commutative, the gauge theory is called non-abelian, like in our case the standard model is. Another example is the Yang-Mills-Theory. [4] Gauge theories are said to have a global symmetry if they are invariant under a transformation identically applied at every point in th ...
... the symmetry group is non-commutative, the gauge theory is called non-abelian, like in our case the standard model is. Another example is the Yang-Mills-Theory. [4] Gauge theories are said to have a global symmetry if they are invariant under a transformation identically applied at every point in th ...
The Lee-Wick Fields out of Gravity
... was argued to be a physical resonance and unitarity is preserved despite the wrong sign in (11). As a result, one is left with a theory containing both massless and massive spin one fields. Similar to photons, the massive Lee-Wick vector fields also serve as mediators of the electromagnetic interac ...
... was argued to be a physical resonance and unitarity is preserved despite the wrong sign in (11). As a result, one is left with a theory containing both massless and massive spin one fields. Similar to photons, the massive Lee-Wick vector fields also serve as mediators of the electromagnetic interac ...
Conclusions Emergent geometry and Chern
... Chinese Academy of Sciences, P.O. Box 2735,Beijing 100190, China ...
... Chinese Academy of Sciences, P.O. Box 2735,Beijing 100190, China ...
The Higgs Boson and Fermion Masses
... three pairs of leptons. They are shown here with their year of discovery. ...
... three pairs of leptons. They are shown here with their year of discovery. ...
The Differential Geometry and Physical Basis for the Application of
... explaining the geometric content of Maxwell’s equations. It was later used to explain Yang-Mills theory and to develop string theory. In 1959 Aharonov and Bohm established the primacy of the vector potential by proposing an electron diffraction experiment to demonstrate a quantum mechanical effect: ...
... explaining the geometric content of Maxwell’s equations. It was later used to explain Yang-Mills theory and to develop string theory. In 1959 Aharonov and Bohm established the primacy of the vector potential by proposing an electron diffraction experiment to demonstrate a quantum mechanical effect: ...
Open-string operator products
... unintegrated vertex operators: Integrated ones are natural from adding backgrounds to the gauge-invariant action; unintegrated ones from adding backgrounds to the BRST operator. We’ll relate the two by going in both directions. The following discussion will be for general quantum mechanics (except i ...
... unintegrated vertex operators: Integrated ones are natural from adding backgrounds to the gauge-invariant action; unintegrated ones from adding backgrounds to the BRST operator. We’ll relate the two by going in both directions. The following discussion will be for general quantum mechanics (except i ...
12.5.2. QCD
... matrices for SU(2). The correspondent gauge theory thus contains 8 independent gauge fields with 8 associated gauge bosons. The latter are called gluons since they glue the quarks together to form hadrons. Like the quarks, these gluons seem to be confined permanently inside the hadrons. Evidence of ...
... matrices for SU(2). The correspondent gauge theory thus contains 8 independent gauge fields with 8 associated gauge bosons. The latter are called gluons since they glue the quarks together to form hadrons. Like the quarks, these gluons seem to be confined permanently inside the hadrons. Evidence of ...
Maxwell-Chern-Simons Theory
... an external uniform B find the spectrum of our theory. The quantization of the Landau problem is well understood, consists of equally spaced energy levels (Landau levels) by ~ωc , B where ωc = m is the cyclotron frequency. Each Landau level is infinitely degenerated in the open plane, but for a fini ...
... an external uniform B find the spectrum of our theory. The quantization of the Landau problem is well understood, consists of equally spaced energy levels (Landau levels) by ~ωc , B where ωc = m is the cyclotron frequency. Each Landau level is infinitely degenerated in the open plane, but for a fini ...