Hamiltonian Mechanics and Symplectic Geometry
... Topics in Representation Theory: Hamiltonian Mechanics and Symplectic Geometry We’ll now turn from the study of specific representations to an attempt to give a general method for constructing Lie group representations. The idea in question sometimes is called “geometric quantization.” Starting from ...
... Topics in Representation Theory: Hamiltonian Mechanics and Symplectic Geometry We’ll now turn from the study of specific representations to an attempt to give a general method for constructing Lie group representations. The idea in question sometimes is called “geometric quantization.” Starting from ...
Lie Algebras and the Schr¨odinger equation: (quasi-exact-solvability, symmetric coordinates) Alexander Turbiner
... (Olshanetsky-Perelomov ’77, Kazhdan-Kostant-Sternberg ’78) ...
... (Olshanetsky-Perelomov ’77, Kazhdan-Kostant-Sternberg ’78) ...
L. Snobl: Representations of Lie algebras, Casimir operators and
... Casimir operator [4]. For its application in the proof of Weyl’s theorem, see [5]. We remark that the quadratic Casimir operator does not exhaust all independent Casimir operators of the semisimple Lie algebra g when we have rank g > 1. It is known that any semisimple Lie algebra ...
... Casimir operator [4]. For its application in the proof of Weyl’s theorem, see [5]. We remark that the quadratic Casimir operator does not exhaust all independent Casimir operators of the semisimple Lie algebra g when we have rank g > 1. It is known that any semisimple Lie algebra ...
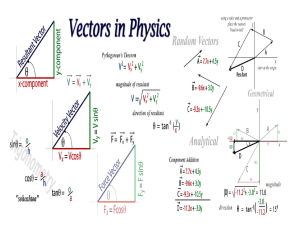
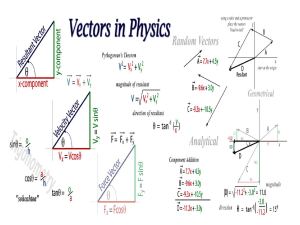
1 Section 1.1: Vectors Definition: A Vector is a quantity that has both
... Applications to Physics and Engineering: A force is represented by a vector because it has both magnitude (measured in pounds or newtons) and direction. If several forces are acting on an object, the resultant force experienced by the object is the vector sum of the forces. EXAMPLE 5: Ben walks due ...
... Applications to Physics and Engineering: A force is represented by a vector because it has both magnitude (measured in pounds or newtons) and direction. If several forces are acting on an object, the resultant force experienced by the object is the vector sum of the forces. EXAMPLE 5: Ben walks due ...
Symmetries in Conformal Field Theory
... if it lands in the subspace of closed forms, so is given by a map to H n−1 (X). In particular this means that charges are independent of the homology class of the codimension 1 submanifold. We’ll use the following fundamental theorem from classical field theory Theorem 1.3 (Noether’s Theorem). There ...
... if it lands in the subspace of closed forms, so is given by a map to H n−1 (X). In particular this means that charges are independent of the homology class of the codimension 1 submanifold. We’ll use the following fundamental theorem from classical field theory Theorem 1.3 (Noether’s Theorem). There ...
Cambridge Paper
... components of the energy-momentum tensor can be obtained as generalized eigenvalues of the Einsten operator. 2. Interaction between singular and nonsingular. ...
... components of the energy-momentum tensor can be obtained as generalized eigenvalues of the Einsten operator. 2. Interaction between singular and nonsingular. ...
Chapter 7 (Lecture 10) Hydrogen Atom The explanation of
... operates in ordinary space only; operates only in spin space. All components of satisfy the same commutation relations. Thus satisfies the same commutation relations as ...
... operates in ordinary space only; operates only in spin space. All components of satisfy the same commutation relations. Thus satisfies the same commutation relations as ...
Topologically Ordered States and their Hamiltonians
... Introduction - The study of topologically ordered states with zero value of the local order parameters is important for classifying various phase states in low-dimensional systems, where the role of quantum fluctuations is significant. In this case, new types of ordering of strongly correlated spin ...
... Introduction - The study of topologically ordered states with zero value of the local order parameters is important for classifying various phase states in low-dimensional systems, where the role of quantum fluctuations is significant. In this case, new types of ordering of strongly correlated spin ...
algebraic quantization and t
... The main purpose of the quantization method (yet another one!) presented in this Letter is to explain this very linkage in a transparent algebraic language, providing a direct connection between the existence of inequivalent quantizations, which we identify with superselection sectors, and the emerg ...
... The main purpose of the quantization method (yet another one!) presented in this Letter is to explain this very linkage in a transparent algebraic language, providing a direct connection between the existence of inequivalent quantizations, which we identify with superselection sectors, and the emerg ...
Spin The evidence of intrinsic angular momentum or spin and its
... and therefore we expect ms to have 2s + 1 disctinct values between −s ≤ ms ≤ s. However, unlike orbital angular momentum quantum number l, the spin angular momentum quantum number can take both integer and half-integer values, s = 0, 1/2, 1, 3/2, 2, . . .. In fact, the experimental result of Stern a ...
... and therefore we expect ms to have 2s + 1 disctinct values between −s ≤ ms ≤ s. However, unlike orbital angular momentum quantum number l, the spin angular momentum quantum number can take both integer and half-integer values, s = 0, 1/2, 1, 3/2, 2, . . .. In fact, the experimental result of Stern a ...
Does Geometric Algebra provide a loophole to Bell`s Theorem?
... (2007); the former focussing on applications in physics, the latter on applications in computer science, especially computer graphics. The wikipedia pages on geometric algebra, and on Clifford algebra, are two splendid mines of information, but the connections between the two sometimes hard to decod ...
... (2007); the former focussing on applications in physics, the latter on applications in computer science, especially computer graphics. The wikipedia pages on geometric algebra, and on Clifford algebra, are two splendid mines of information, but the connections between the two sometimes hard to decod ...
PHYSICS
... Place first vector on graph with tail starting at the origin Place the second vector with the tail at the tip of the first vector Repeat step two for multiple vectors Draw a line from the tail of the first vector to the tip of the final vector. This final -x vector is called the resultant. The order ...
... Place first vector on graph with tail starting at the origin Place the second vector with the tail at the tip of the first vector Repeat step two for multiple vectors Draw a line from the tail of the first vector to the tip of the final vector. This final -x vector is called the resultant. The order ...
On-Shell Methods in Quantum Field Theory
... events have high multiplicity of hard clusters (jets) each jet has a high multiplicity of hadrons higher-order perturbative corrections are important ...
... events have high multiplicity of hard clusters (jets) each jet has a high multiplicity of hadrons higher-order perturbative corrections are important ...
Single crystal growth of Heisenberg spin ladder and spin chain
... Low dimensional magnets have attracted great attention because of their simplicity in theoretical models, novel quantum phenomena and relation to high temperature superconductivity. Among them, quasi-1D systems such as spin ladders and spin chains have found their realization in several materials, e ...
... Low dimensional magnets have attracted great attention because of their simplicity in theoretical models, novel quantum phenomena and relation to high temperature superconductivity. Among them, quasi-1D systems such as spin ladders and spin chains have found their realization in several materials, e ...