Discrete Joint Distributions
... solve(t(X01) %*% X01) %*% t(X01) %*% Y See regression.R . Estimating the variance The maximum likelihood estimate for the variance is ...
... solve(t(X01) %*% X01) %*% t(X01) %*% Y See regression.R . Estimating the variance The maximum likelihood estimate for the variance is ...
Chapter 11 course notes
... • Often, however, we gather data on two random variables. • We wish to determine: Is there a relationship between the two r.v.’s? • Can we use the values of one r.v. to predict the other r.v.? • Often we assume a straight-line relationship between two variables. • This is known as simple linear regr ...
... • Often, however, we gather data on two random variables. • We wish to determine: Is there a relationship between the two r.v.’s? • Can we use the values of one r.v. to predict the other r.v.? • Often we assume a straight-line relationship between two variables. • This is known as simple linear regr ...
Slide 1
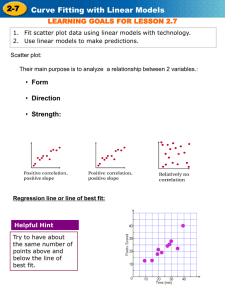
... 1. Fit scatter plot data using linear models with technology. 2. Use linear models to make predictions. Scatter plot: Their main purpose is to analyze a relationship between 2 variables.: ...
... 1. Fit scatter plot data using linear models with technology. 2. Use linear models to make predictions. Scatter plot: Their main purpose is to analyze a relationship between 2 variables.: ...
e388_10_Win_Final
... c) Measurement Error (using Instrumental Variables), can all be viewed as regressing TY on TX for the following linear model: Y X In each of the three cases, indicate what the T matrix is that is pre-multiplied through the model to make the respective correction (make clear whatever addition ...
... c) Measurement Error (using Instrumental Variables), can all be viewed as regressing TY on TX for the following linear model: Y X In each of the three cases, indicate what the T matrix is that is pre-multiplied through the model to make the respective correction (make clear whatever addition ...
Inference in Linear Regression There are four basic assumptions
... 4. The normal distribution of Y values corresponding to a particular value of X has standard deviation σ{Y |X}. That standard deviation is usually assumed to be the same for all values of X so that we may write σ{Y |X} = σ. ...
... 4. The normal distribution of Y values corresponding to a particular value of X has standard deviation σ{Y |X}. That standard deviation is usually assumed to be the same for all values of X so that we may write σ{Y |X} = σ. ...
on Assumptions in Correlation and Regression
... change with X. This assumption can be restated in terms of the error term: the distribution of the error term (the residuals) is normal at every value of X and constant in variance across values of X. Pedhazur (1982) stated the assumptions of regression analysis as follows: ...
... change with X. This assumption can be restated in terms of the error term: the distribution of the error term (the residuals) is normal at every value of X and constant in variance across values of X. Pedhazur (1982) stated the assumptions of regression analysis as follows: ...
Coefficient of determination
In statistics, the coefficient of determination, denoted R2 or r2 and pronounced R squared, is a number that indicates how well data fit a statistical model – sometimes simply a line or a curve. An R2 of 1 indicates that the regression line perfectly fits the data, while an R2 of 0 indicates that the line does not fit the data at all. This latter can be because the data is utterly non-linear, or because it is random.It is a statistic used in the context of statistical models whose main purpose is either the prediction of future outcomes or the testing of hypotheses, on the basis of other related information. It provides a measure of how well observed outcomes are replicated by the model, as the proportion of total variation of outcomes explained by the model (pp. 187, 287).There are several definitions of R2 that are only sometimes equivalent. One class of such cases includes that of simple linear regression where r2 is used instead of R2. In this case, if an intercept is included, then r2 is simply the square of the sample correlation coefficient (i.e., r) between the outcomes and their predicted values. If additional explanators are included, R2 is the square of the coefficient of multiple correlation. In both such cases, the coefficient of determination ranges from 0 to 1.Important cases where the computational definition of R2 can yield negative values, depending on the definition used, arise where the predictions that are being compared to the corresponding outcomes have not been derived from a model-fitting procedure using those data, and where linear regression is conducted without including an intercept. Additionally, negative values of R2 may occur when fitting non-linear functions to data. In cases where negative values arise, the mean of the data provides a better fit to the outcomes than do the fitted function values, according to this particular criterion.